Предыдущая страница реферата | 1  2  3  4  5  6  7 | Следующая страница реферата

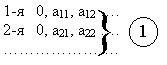
Возьмем произвольное число 0,b1,b2,b3

b1 ¹ a11, b2 ¹ a22, …

Эта дробь не может выйти в последовательность т.к. отличается от всех чисел, значит нельзя пронумеровать числа на отрезке [0;1].

Множество нечетно и называется континуальным, а его мощность континуум.

Метод, используемый при доказательстве, называется диагональным методом Кантора.

Отношение

Пусть дано RÍ Mn – n местное отношение на множество М.

Будем изучать двухместные или бинарные отношения. Если а и b находятся в отношении R, то записывается а R b.

Проведем отношение на множество N:

А) отношение £ выполняется для пар (7,9) (7,7_

Б) (9,7) не выполняется.

Пример отношения на множество R

А) отношение находится на одинаковом расстоянии от начала координат выполняется для пар (3; 4) и (2; Ö 21)

Б) (3; 4) и (1; 6) не выполняется.

Для задания бинарных отношений можно использовать любые способы задания множеств.

Для конечных множеств используют матричный способ задания множеств.

Матрица бинарного отношения на множество M={1;2;3;4}, тогда матрица отношения С равна

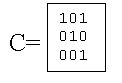
Отношение Е заданные единичной матрицей называется отношением равенства.

Отношением назовется обратным к отношением R, если ajRai тогда и только тогда, когда ajRai обозначают R-1.

Свойства отношений

1.Если aRa ==> очн. рефлексивное и матрица содержит на главной диагонали единицу

если ни для какого а не … ==> отношение антирефлексивное

главная диагональ содержит нули

Пр. отношнний

£ рефлексивное

Рекомендуем скачать другие рефераты по теме: контрольная работа 10 класс, контрольная работа 8.





Предыдущая страница реферата | 1  2  3  4  5  6  7 | Следующая страница реферата