Предыдущая страница реферата | 4  5  6  7  8  9  10  11  12  13  14 | Следующая страница реферата

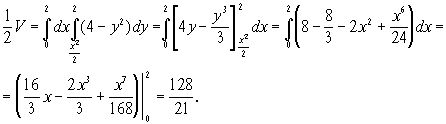
Следовательно, куб.ед.

4) Вычислим объём V тела, ограниченного поверхностью и плоскостью Oxy.

Заданное тело представляет собой сегмент эллиптического

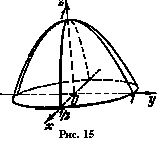
параболоида, расположенный над плоскостью Оху (рис.15). Параболоид пересекается с плоскостью Оху по эллипсу

Следовательно, задача состоит в отыскании объема цилиндрического тела, имеющего своим основанием внутренность указанного эллипса и ограниченного параболоидом

В силу симметрии тела относительно плоскостей Oxz и Oyz можно вычислить объем четвертой его части, заключенной в первом координатном угле. Этот объем равен двойному интегралу, распространенному по области, заданной условиями т. е. по четверти эллипса. Интегрируя сначала по у, затем по х, получим

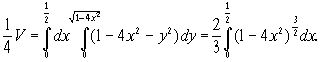
Подстановка даёт

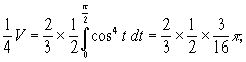
откуда

 

3.Приложения двойных интегралов к задачам

механики.

а) Масса плоской пластинки переменной плотности.

Рассмотрим тонкую пластинку, расположенную на плоскости Оху и занимающую область D. Толщину этой пластинки считаем настолько малой, что изменением плотности по толщине ее можно пренебречь.

Поверхностной плотностью такой пластинки в данной точке называется предел отношения массы площадки к ее площади при условии, что площадка стягивается к данной точке.

Определенная таким образом поверхностная плотность будет зависеть только от положения данной точки, т. е. являться функцией ее координат:

 

Если бы плотность была постоянной (), то масса всей пластинки равнялась бы , где S - площадь пластинки. Найдем теперь массу неоднородной пластинки, считая, что ее плотность является заданной функцией . Для этого разобьем область, занимаемую пластинкой, на частичные области с площадями (рис. 16). Выбирая в каждой частичной области произвольную точку , будем считать, что плотность во всех точках частичной области постоянна и равна плотности в выбранной точке. Составим приближенное выражение для массы пластинки в виде интегральной суммы

(*)

Рекомендуем скачать другие рефераты по теме: доклад по химии, банк рефератов и курсовых.





Предыдущая страница реферата | 4  5  6  7  8  9  10  11  12  13  14 | Следующая страница реферата