Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9 | Следующая страница реферата

имеет решения.

Решение.

Из первого уравнения системы получим 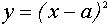при 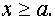Следовательно, это уравнение задаёт семейство “полупарабол” - правые ветви параболы 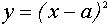“скользят” вершинами по оси абсцисс.

Выделим в левой части второго уравнения полные квадраты и разложим её на множители

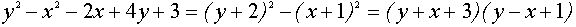
Множеством точек плоскости 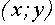, удовлетворяющих второму уравнению, являются две прямые

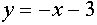и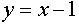

Выясним, при каких значениях параметра а кривая из семейства “полупарабол” имеет хотя бы одну общую точку с одной из полученных прямых.

Если вершины полупарабол находятся правее точки А, но левее точки В (точка В соответствует вершине той “полупараболы”, которая касается

прямой 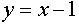), то рассматриваемые графики не имеют общих точек. Если вершина “полупараболы” совпадает с точкой А, то .

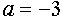Случай касания “полупараболы” с прямой 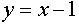определим из условия существования единственного решения системы

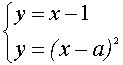
В этом случае уравнение

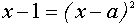
имеет один корень, откуда находим :

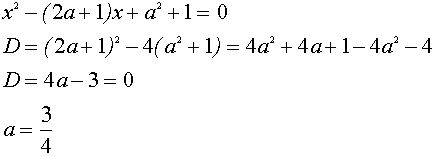
Следовательно, исходная система не имеет решений при 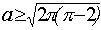, а пр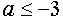и или 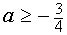имеет хотя бы одно решение.

Ответ: а Î (-¥ ;-3] È (;+¥ ).

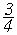IV. Решить уравнение

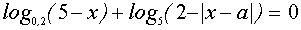
Решение.

Использовав равенство 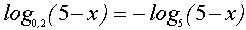, заданное уравнение перепишем в виде

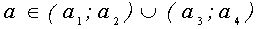
Это уравнение равносильно системе

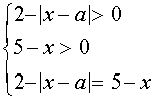
Рекомендуем скачать другие рефераты по теме: реферат на тему человек, диплом на заказ.





Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9 | Следующая страница реферата