
Графическое решение уравнений, неравенств, систем с параметром
| Категория реферата: Рефераты по математике
| Теги реферата: контрольная работа 8, шпори на пятках
| Добавил(а) на сайт: Хребтов.
Предыдущая страница реферата | 1 2 3 4 5 6 7 8 9 | Следующая страница реферата
§ 2. Алгоритм решения. Находим область определения уравнения. Выражаем a как функцию от х. В системе координат хОа строим график функции а=¦ (х) для тех значений х, которые входят в область определения данного уравнения.
Находим точки пересечения прямой а=с, где сÎ (-¥ ;+¥ ) с графиком функции а=¦ (х).Если прямая а=с пересекает график а=¦ (х), то определяем абсциссы точек пересечения. Для этого достаточно решить уравнение а=¦ (х) относительно х.
Записываем ответ. § 3. ПримерыI. Решить уравнение
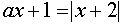 (1)
(1)
Решение.
Поскольку х=0 не является корнем уравнения, то можно разрешить уравнение относительно а :
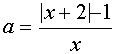 или
или 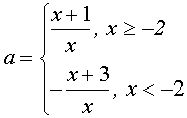
График функции – две “склеенных” гиперболы. Количество решений исходного уравнения определяется количеством точек пересечения построенной линии и прямой у=а.
Если а Î
(-¥
;-1]È
(1;+¥
)È
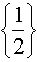 , то прямая у=а пересекает график уравнения (1) в одной точке. Абсциссу этой точки найдем при решении уравнения
, то прямая у=а пересекает график уравнения (1) в одной точке. Абсциссу этой точки найдем при решении уравнения 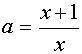 относительно х.
относительно х.
Таким образом, на этом промежутке уравнение (1) имеет решение 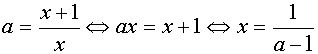 .
.
Если а Î
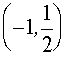 , то прямая у=а пересекает график уравнения (1) в двух точках. Абсциссы этих точек можно найти из уравнений
, то прямая у=а пересекает график уравнения (1) в двух точках. Абсциссы этих точек можно найти из уравнений 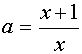 и
и 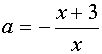 , получаем
, получаем
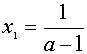 и
и 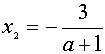 .
.
Если а Î
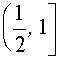 , то прямая у=а не пересекает график уравнения (1), следовательно решений нет.
, то прямая у=а не пересекает график уравнения (1), следовательно решений нет.
Ответ:
Если а Î
(-¥
;-1]È
(1;+¥
)È
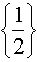 , то
, то 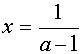 ;
;
Если а Î 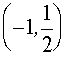 ,
то
,
то 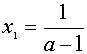 ,
, 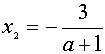 ;
;
Если а Î
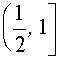 , то решений нет.
, то решений нет.
II. Найти все значения параметра а, при которых уравнение 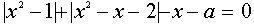 имеет три различных корня.
имеет три различных корня.
Решение.
Переписав уравнение в виде 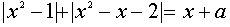 и рассмотрев пару функций
и рассмотрев пару функций 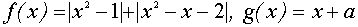 , можно заметить, что искомые значения параметра а и только они будут соответствовать тем положениям графика функции
, можно заметить, что искомые значения параметра а и только они будут соответствовать тем положениям графика функции 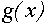 , при которых он имеет точно три точки пересечения с графиком функции
, при которых он имеет точно три точки пересечения с графиком функции 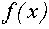 .
.
В системе координат хОу построим график функции 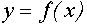 ). Для этого можно представить её в виде
). Для этого можно представить её в виде 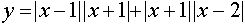 и, рассмотрев четыре возникающих случая, запишем эту функцию в виде
и, рассмотрев четыре возникающих случая, запишем эту функцию в виде
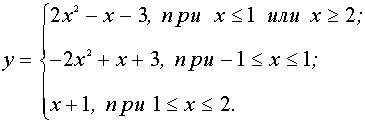
Поскольку график функции 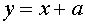 – это прямая, имеющая угол наклона к оси Ох, равный
– это прямая, имеющая угол наклона к оси Ох, равный 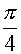 , и пересекающая ось Оу в точке с координатами (0 , а), заключаем, что три указанные точки пересечения можно получить лишь в случае, когда эта прямая касается графика функции
, и пересекающая ось Оу в точке с координатами (0 , а), заключаем, что три указанные точки пересечения можно получить лишь в случае, когда эта прямая касается графика функции 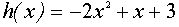 . Поэтому находим производную
. Поэтому находим производную 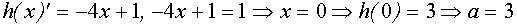
Ответ: 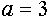 .
.
III. Найти все значения параметра а, при каждом из которых система уравнений
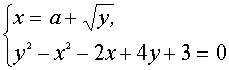
Рекомендуем скачать другие рефераты по теме: реферат на тему человек, диплом на заказ.
Категории:
Предыдущая страница реферата | 1 2 3 4 5 6 7 8 9 | Следующая страница реферата
 Главная
Главная