Интеграл Пуассона

Пусть ¦ ( x) , g(x) , xÎ R1 –суммируемые на [ -p , p ] , 2p - периодические, комплекснозначные функции. Через f* g(x) будем обозначать свертку

f* g(x) =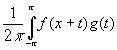dt

Из теоремы Фубини легко следует, что свертка суммируемых функций также суммируема на [ -p ,p ] и

cn ( f* g ) = cn ( f )× cn ( g ) , n = 0, ± 1 , ± 2 , ... ( 1 )

где { cn ( f )} -- коэффициенты Фурье функции f ( x ) :

cn = 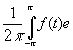-i n tdt , n = 0, ± 1 , ± 2 , ¼

Пусть ¦ Î L1 (-p , p ) . Рассмотрим при 0 £ r < 1 функцию

¦ r ( x ) = 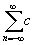n ( f ) r| n | ei n x , x Î [ - p , p ] , ( 2 )

где ряд в правой части равенства (2) сходится равномерно по х для любого фиксированного r , 0 £ r < 1 . Коэффициенты Фурье функции ¦ r ( х) равны

cn ( fr ) = cn × r| n | , n = 0 , ± 1 , ± 2 , ¼ , а это согласно (1) значит, что ¦ r ( x ) можно представить в виде свертки :

¦ r ( x ) = 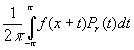, ( 3 )

где

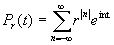, t Î [ - p , p ] . ( 4 )

Функция двух переменных Рr (t) , 0 £ r < 1 , t Î [ - p , p ] , называется ядром Пуассона , а интеграл (3) -- интегралом Пуассона .

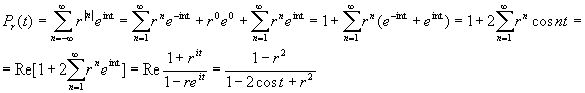
Следовательно,

Pr ( t ) = 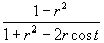, 0 £ r < 1 , t Î [ - p , p ] . ( 5 )

Если ¦ Î L1 ( -p , p ) - действительная функция , то , учитывая , что

c-n ( f ) = ` cn( f ) , n = 0, ± 1 , ± 2 , ¼ , из соотношения (2) мы получим :

fr ( x ) =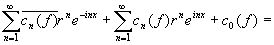

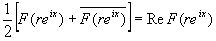= , ( 6 )

где

F ( z ) = c0 ( f ) + 2 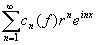( z = reix ) ( 7 )

аналитическая в единичном круге функция . Равенство (6) показывает, что для любой действительной функции ¦ Î L1( -p , p ) интегралом Пуассона (3) определяется гармоническая в единичном круге функция

u ( z ) = ¦ r (eix ) , z = reix , 0 £ r < 1 , x Î [ -p , p ] .

При этом гармонически сопряженная с u (z) функция v (z) c v (0) = 0 задается формулой

Рекомендуем скачать другие рефераты по теме: реферат египет, культурология шпаргалки.





1  2  3  4 | Следующая страница реферата