Предыдущая страница реферата | 1  2  3  4 | Следующая страница реферата

.

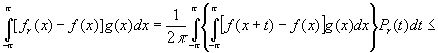
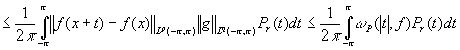Следовательно,

.

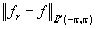
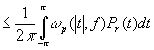Для данного e > 0 найдем d = d (e ) такое, что 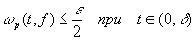. Тогда для r , достаточно близких к единице, мы получим оценку

.

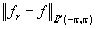
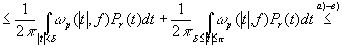
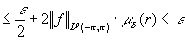Аналогично второе неравенство вытекает из неравенства

.

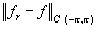
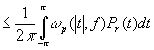Теорема 1 доказана.

Дадим определения понятий "максимальная функция" и "оператор слабого типа", которые понадобятся нам в ходе доказательства следующей теоремы.

Определение1.

Пусть функция 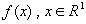суммируема на любом интервале (-А, А), А > 0 . Максимальной функцией для функции 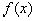называется функция

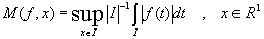
где супремум берется по всем интервалам I , содержащим точку х.

Определение 2.

Оператор 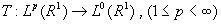называется оператором слабого типа (р,р) , если для любого y > 0

.

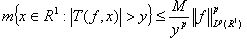Теорема 2 (Фату).

Пусть 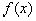- комплекснозначная функция из 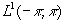. Тогда

для п.в. .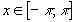

Доказательство.

Покажем, что для 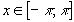и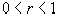

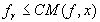, ( 13 )

где С - абсолютная константа , а M ( f, x ) - максимальная функция для f (x) . Для этой цели используем легко выводимую из (5) оценку

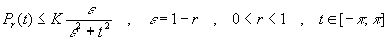
Рекомендуем скачать другие рефераты по теме: реферат египет, культурология шпаргалки.





Предыдущая страница реферата | 1  2  3  4 | Следующая страница реферата