Предыдущая страница реферата | 1  2  3  4 | Следующая страница реферата

v (z) = Im F (z) = 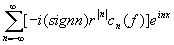. ( 8 )

Утверждение1.

Пусть u (z) - гармоническая ( или аналитическая ) в круге | z | < 1 + e ( e > 0 ) функция и ¦ (x) = u (eix) , xÎ [ - p , p ] . Тогда

u (z) = 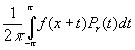( z = reix , | z | < 1 ) ( 10 ).

Так как ядро Пуассона Pr (t) - действительная функция, то равенство (10) достаточно проверить в случае, когда u (z) - аналитическая функция:

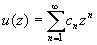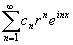=, | z | < 1 + e .

Но тогда

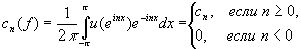
и равенство (10) сразу следует из (2) и (3).

Прежде чем перейти к изучению поведения функции ¦ r (x) при r® 1 , отметим некоторые свойства ядра Пуассона:

а) ;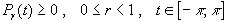

б) ;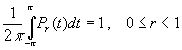

в) для любого d >0

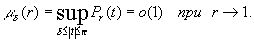
Соотношения а) и в) сразу следуют из формулы (5), а для доказательства б) достаточно положить в (2) и (3) ¦ ( х) º 1 .

Теорема 1.

Для произвольной (комплекснозначной) функции 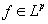( -p , p ) , 1 £ p < ¥ , имеет место равенство

;

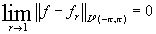если же ¦ (x) непрерывна на [ -p , p ] и ¦ (-p ) = ¦ (p ) , то

.

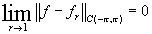Доказательство.

В силу (3) и свойства б) ядра Пуассона

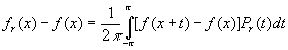( 12 )

Для любой функции 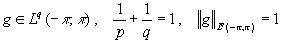, пользуясь неравенством Гельдера и положительностью ядра Пуассона , находим

 

Рекомендуем скачать другие рефераты по теме: реферат египет, культурология шпаргалки.





Предыдущая страница реферата | 1  2  3  4 | Следующая страница реферата