|
0
|
353
|
|
0,00386
|
343
|
|
0,00772
|
313
|
|
0,01158
|
261
|
|
0,01544
|
184
|
|
0,01930
|
74
|
2. Обработка результатов эксперимента.
2.1 Задача регрессии. Метод наименьших квадратов.
Ищем функцию регрессии в виде (1.1). Оценки
коэффициентов находим с помощью МНК, при этом наименьшими будут оценки, обеспечивающие минимум квадратов отклонений оценочной функции регрессии от
экспериментальных значений температуры; суммирование ведут по всем
экспериментальным точкам, т.е. минимум величины S:
(2.1)
В нашем случае необходимым т достаточным
условием минимума S будут:
Где k = 0, 1, 2. (2,2)
Из уравнений (2.1) и (2.2) получаем:
(2.3)
Сумма
Система (2.3) примет вид:
(2.4)
В результате вычислений получаем Sk и Vj.
Обозначим матрицу коэффициентов уравнения (2.4) через “p”:
Методом Гаусса решаем систему (2.4) и найдём
обратную матрицу p-1. В результате получаем:
Подставляя в (2.1) найденные значения оценок
коэффициентов ак, находим минимальное значение суммы S:
Smin=0.7597
Рекомендуем скачать другие рефераты по теме: реферат по труду, педагогические рефераты.
Предыдущая страница реферата |
1
2
3
4
5
6
7
8
9
10
11 |
Следующая страница реферата
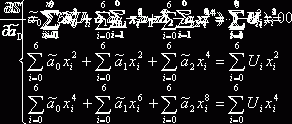
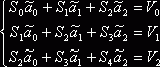
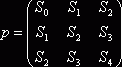
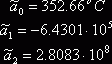
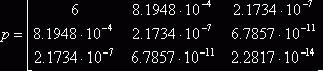
 Главная
Главная