
Исследование распределения температуры в тонком цилиндрическом стержне
| Категория реферата: Рефераты по математике
| Теги реферата: экзамен, защита диплома
| Добавил(а) на сайт: Derevskov.
Предыдущая страница реферата | 1 2 3 4 5 6 7 8 9 10 11 | Следующая страница реферата
, где M[f”(t)], t e [0;T], f(t)=e-bt3
Учитывая формулу (3.4) получаем:
(3.5)
Дифференцируя f(t), получим:
А необходимое условие экстремума: f”(t)-f’’’(t)=0, откуда получаем:
Далее вычисляем значения f’’(t) при t=t1, t=t2, t=0 и t=T, получаем:
f’’(t1)=1.5886 10-4
f’’(t2)=-1.6627 10-4
f’’(0)=0
f’’(T)=7.4782 10-6
Итак: M1,5886 10-4, откуда n=25.66; принимаем N=26.
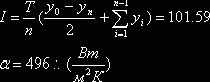 |
Далее вычислим интеграл I:
Погрешность вычисления :
3.2 Вычисление интеграла I методом парабол
При расчётах будем использовать теоретическую оценку погрешности с помощью правила Рунге. Для обеспечения заданной точности количество частей n, на которое следует разделить интервал интегрирования можно определить по формуле:
, откуда:
Нахождение М4 можно провести аналогично нахождению М2 в предыдущем пункте, но выражение для fIV(t) имеет довольно громоздкий вид. Поэтому правило Рунге – наиболее простой способ.
Обозначим через In и I2n значение интеграла I, полученное при разбиении промежутка интегрирования соответственно на n и 2n интервалов. Если выполнено равенство: |I2n-In| = 15 , то |I-I2n|=
Будем , начиная с n=2, удваивать n до тех пор, пока не начнёт выполняться неравенство (*1), тогда:
(3.6)
Согласно формуле парабол (3.7):
Результаты вычислений сведём в таблицу:
|
n |
In Рекомендуем скачать другие рефераты по теме: реферат по труду, педагогические рефераты. Категории:Предыдущая страница реферата | 1 2 3 4 5 6 7 8 9 10 11 | Следующая страница реферата Поделитесь этой записью или добавьте в закладки |
|
 Главная
Главная