Предыдущая страница реферата | 1  2  3  4 | Следующая страница реферата

 Отметим, что вблизи различных точек кривая искривлена по-разному. Для того чтобы охарактеризовать степень искривлённости данной линии в непосредственной близости к данной точке А, введём понятие кривизны в данной точке.

Определение5.  Кривизной Ка линии в данной точке А называется предел средней кривизны дуги АВ, когда длина этой дуги стремится к нулю:

Вычисление кривизны

Выведем формулу для вычисления кривизны данной линии в любой её точке M(x, y).  При этом  будем предполагать, что кривая задана в декартовой системе координат уравнением вида  y=f(x)  и что функция имеет непрерывную вторую производную.

Проведём касательные к кривой в точках  M и M1 с абсциссами   x  и  x+Dx и  обозначим через  j и j+Dj  углы наклона этих касательных (рис.7).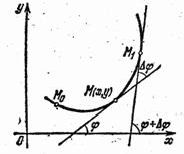

Длину дуги ÈM0M отсчитываемую от некоторой постоянной точки M0, обозначим через s; тогда Ds = ÈM0M1 -  ÈM0M, а½Ds½ = ÈMM1.   Как видно из (рис. 7), угол смежности, соответствующий дуге  ÈMM1   равен абсолютной величине  разности углов  j   и  j+Dj, то есть равен ½Dj½.

Согласно определению средней кривизны кривой на участке  ÈMM1  имеем .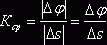

Чтобы получить кривизну в точке М, нужно найти предел полученного выражения при условии, что длина дуги ÈMM1 стремится к нулю:

Так как величины j и s зависят от x, то, следовательно, j  можно рассматривать как функцию от s. Можно считать, что эта функция задана параметрически с помощью параметра x. Тогда

         

Для вычисления  воспользуемся формулой дифференцирования функции, заданной параметрически:    .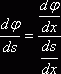

Чтобы выразить производную   через функцию  y=f(x),  заметим,  что   и, следовательно  .

Дифференцируя по x последнее равенство,  получаем        .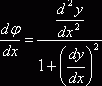

И так как 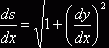            , то

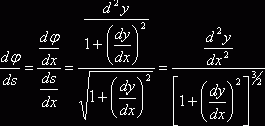,  и окончательно, так как , получаем

.

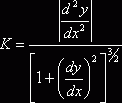Следовательно, в любой точке кривой, где существует и непрерывна вторая производная, можно вычислить кривизну по формулам.

Вычисление кривизны линии, заданной параметрически.

Пусть кривая задана параметрически: x=j(t),  y=y(t).  Тогда

  

Подставляя полученные выражения в формулу 3, получаем

.

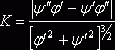Вычисление кривизны линии, заданной уравнением в полярных координатах.

Пусть кривая задана уравнением вида r = f(q). Запишем формулы перехода от полярных координат к декартовым: x = r cos q, y = r sin q .

Если в эти формулы подставить вместо r его выражение через q, то есть f(q), то получим

x = f(q) cos q, y = f(q) sin q

Последние уравнения можно рассматривать как параметрические уравнения кривой, причём параметром является q.

Рекомендуем скачать другие рефераты по теме: мини сочинение, детские рефераты.





Предыдущая страница реферата | 1  2  3  4 | Следующая страница реферата