Предыдущая страница реферата | 1  2  3  4

Тогда,       

 ,         

Подставляя последние выражения в формулу, получаем формулу для вычисления кривизны кривой, заданной в полярных координатах:

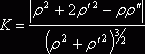
Радиус и круг кривизны

Определение 7.   Величина R, обратная кривизне К линии в данной точке М, называется радиусом кривизны этой линии в рассматриваемой точке:  R = 1/K,   или 

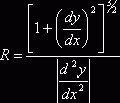
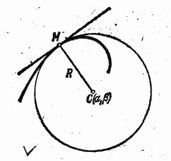
Построим в точке М нормаль к кривой (рис. 8 ), направленную в сторону вогнутости кривой, и отложим на этой нормали отрезок МС, равный радиусу R кривизны кривой в точке М.

Точка С называется центром кривизны данной кривой с центром в точке С (проходящий через точку М) называется кругом кривизны данной кривой в точке М.

Из определения круга кривизны следует, что в данной точке кривизна кривой и кривизна круга кривизны равны между собой. Выведем формулы, определяющие координаты центра кривизны.

Пусть кривая задана уравнением y=f(x). Зафиксируем на кривой точку M(x, y) и определим координаты  a  и b   центра кривизны, соответствующего этой точке (рис. 9).Для этого напишем уравнение нормали к кривой в точке М:

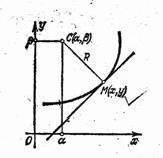
Так как точка C(a, b) лежит на нормали, то её координаты должны удовлетворять уравнению    .

Далее, точка  C(a, b)  находится от точки М на расстоянии, равном радиусу кривизны R:

Решив совместно уравнения * определим a, b:

                         

                                         

и так как 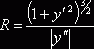  ,   то

                                              

Чтобы решить вопрос о том, верхние или нижние знаки сле6дует брать в последних формулах, нужно рассмотреть случай y!!>0  и y!!0 , то в этой точке кривая вогнута и, следовательно, b>y (рис. 9) и поэтому следует брать нижние знаки. Учитывая, что в этом случае ½y!!½= y!!, формулы координат центра запишем в следующем виде:

                                                 (1)

Аналогично можно показать, что формулы будут справедливы и в случае y!!

Скачали данный реферат: Янцев, Tukaj, Savenkov, Убыш, Стрекалов, Митин.
Последние просмотренные рефераты на тему: доклад по информатике, реферат русь, педагогические рефераты, творчество реферат.

Предыдущая страница реферата | 1  2  3  4