Математическое ожидание и дисперсия для интервальных и пропорциональных шкал. Доверительные интервалы

| Категория реферата: Рефераты по математике
| Теги реферата: контрольные 2 класс, физика и техника
| Добавил(а) на сайт: Райков.

Рассмотрим ситуацию, когда необходимо сравнить две группы из n человек первая и N вторая: например, экспериментальную и контрольную - две группы детей, обучающихся по разным методикам. Правильность составления этих групп мы сейчас не будем подвергать сомнению и будем считать их случайными выборками.

В отличие от мышления на уровне обыденного сознания, склонного воспринимать полученную в результате опыта разность средних как факт и основание для вывода, более вдумчивый исследователь не будет торопиться. Ведь всегда остается возможность случайности различий и отсутствия значимой разницы в числах, например, средних mx и стандартных ошибок s x. Поэтому в начале придется выдвинуть статистическую гипотезу об отсутствии значимых различий, которую назовем нулевой гипотезой. По отношению к средним эта гипотеза следующая: и в первой и во второй группах mx=M, где число М можно назвать теоретическим средним.

Логика проверки подобных статистических гипотез определяется тем, что всегда есть риск ошибиться в выводах и неправильно отвергнуть правильную гипотезу. Обозначим a - вероятность ошибочно отвергнуть правильную гипотезу, или уровень значимости, а р=1- a назовем доверительной вероятностью. Величину a исследователь выбирает произвольно в зависимости от конкретной ситуации. Например, a =0,05 (или 5%) означает риск ошибиться в 5 случаях из 100.

Как известно, гипотеза отвергается, если в эксперименте наблюдается явление, противоречащее этой гипотезе. Наоборот, если в эксперименте встретилось явление, не противоречащее гипотезе, это еще не означает ее доказательства. Таким образом, отвержение гипотезы гораздо более надежно, в противном же случае можно говорить только, что наблюдения не противоречат гипотезе.

В статистике приходится считать явление противоречащим гипотезе, если вероятность его появления мала (а именно равна a ). Остается теперь только выяснить, чтоже это за явление.

Посмотрев на формулу для математического ожидания mx, можно увидеть, что эта величина есть не что иное, как сумма большого числа случайных величин - отдельных наблюдений. Поэтому в силу центральной предельной теоремы величина mx подчиняется нормальному закону (см. рис.1), со средним (теоретическим) М и неизвестным стандартным отклонением S. Можно доказать, что S в Ц n раз меньше стандартного отклонения каждого отдельного наблюдения, для оценки которого можно использовать величину s х. Поэтому по правилу “трех s “ для Z - закона получаем, что с доверительной вероятностью р=0,997:

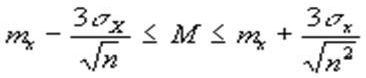
а для р=0,95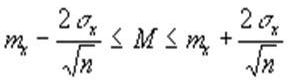

которые называются доверительными интервалами для теоретической средней М. Ясно, что если доверительные интервалы для М из двух групп не пересекаются, то нулевую гипотезу следует отвергнуть.

Например, опросили еще одну группу из N =9 человек и получили следующее число правильных ответов: