Метод АВИ в математической теории переноса вредных веществ в гетерогенных средах

С.н.с. Алехин В. И.

Кафедра автоматизированной обработки информации.

Северо-Кавказский горно-металлургический институт (государственный технологический университет)

Метод решения дифференциальных уравнений, разработанный В. И. Алехиным (метод АВИ), применяется для определения переноса вредных веществ в гетерогенных средах.

В работах [1 – 3] была отмечена специфика метода АВИ при решении задач по определению переноса вредных веществ под действием импульсных источников в гомогенных средах.

При непосредственном применении метода АВИ для изучения вопроса распространения вредных веществ в гетерогенных средах возникают трудности, связанные с наличием двухпараметрического асимптотического решения исходного уравнения при

Для преодоления этой проблемы в настоящей работе вводятся разные масштабы  и . Здесь  характерный масштаб изменения времени импульсного выброса, характерный масштаб (параметр) изменения неоднородностей гетерогенной среды, в которой распространяются вредные вещества после импульсного выброса.

Проиллюстрируем применение метода АВИ на следующем примере.

Пусть имеем уравнение, которое описывает диффузию вредных веществ, вызванную периодическим импульсным источником (действующим в моменты времени :

 , (1)

здесь периодические (период равен – 1), ограниченные , гладкие функции по  где

Учитывая, что при  имеет место импульсный выброс вредных веществ, определяем поведение их концентрации при  Для этого применим метод АВИ, согласно которому будем иметь асимптотическое решение уравнения (1) в следующем виде:

 , (2)

где   и т.д. – гладкие, ограниченные функции по Подставим (2) в уравнение (1) и приравняем нулю коэффициенты при .

В результате получим следующую систему рекуррентных, дифференциальных уравнений, из которой определяются коэффициенты асимптотического разложения (2):  

 …….и.т.д. (3)

Здесь  ; ;

;  ….. и т. д. (4)

Рассмотрим первое уравнение системы (3), (4)

. (5)

Будем искать в следующем виде , тогда

.

Проинтегрируем последнее уравнение по  , в результате найдем

, (6)

 , .

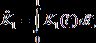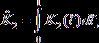Рекомендуем скачать другие рефераты по теме: бесплатно решебник, зимой сочинение.





1  2  3  4 | Следующая страница реферата