Метод бесконечного спуска

| Категория реферата: Рефераты по математике
| Теги реферата: здоровый образ жизни реферат, реферат обслуживание
| Добавил(а) на сайт: Митасов.

В заключение — задача на клетчатой бумаге.

Задача 6. Дан лист клетчатой бумаги. Доказать, что при n ≠ 4 не существует правильного n-угольника с вершинами в узлах решётки.

Решение. Вначале докажем, что не существует правильного треугольника с вершинами в узлах. Действительно, пусть a — длина стороны этого треугольника; тогда a2 — целое число по теореме Пифагора. Площадь треугольника равна a2√3/4, то есть иррациональна. С другой стороны, очевидно, что площадь любого многоугольника с вершинами в узлах рациональна.

Поскольку в правильный шестиугольник можно вписать правильный треугольник с вершинами в его вершинах, для n = 6 утверждение тоже доказано.

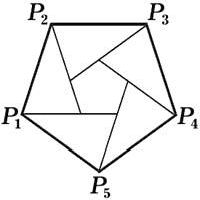
Пусть n ≠ 3, 4, 6. Допустим, что P1, P2, ..., Pn — n-угольник с вершинами в узлах. Отложим от точек P1, P2, ..., Pn векторы, соответственно равные векторам P2P3, P3P4, ..., P1P2 (см. рис.). Новые точки вновь попадут в узлы решётки и образуют правильный n-угольник внутри первоначального. С новым n-угольником можно поступить так же, и так далее, без конца. Однако квадрат длины стороны n-угольника — целое число, а при наших постороениях оно всё время уменьшается!