Если окажется, что 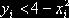 , то точка
, то точка 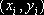 лежит под кривой
лежит под кривой 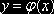 и в «счётчик
и в «счётчик 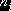 » надо добавить единицу.
» надо добавить единицу.
Результаты десяти испытаний приведены в таблице 3.
Из таблицы 3 находим 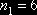 . Искомая оценка интеграла
. Искомая оценка интеграла
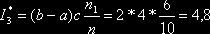
§5. Способ «выделения главной части».
В качестве оценки интеграла 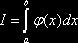 принимают
принимают
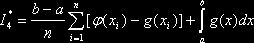 ,
,
где 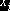 - возможные значения
случайной величины X, распределённой равномерно в интервале интегрирования
- возможные значения
случайной величины X, распределённой равномерно в интервале интегрирования 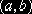 , которые разыгрывают по формуле
, которые разыгрывают по формуле 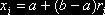 ; функция
; функция 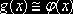 , причём интеграл
, причём интеграл 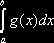 можно вычислить
обычными методами.
можно вычислить
обычными методами.
Задача. Найти оценку 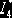 интеграла
интеграла 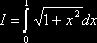 .
.
Решение. Так как 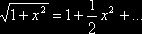
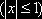 , то примем
, то примем 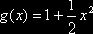 . Тогда, полагая число испытаний n=10, имеем оценку
. Тогда, полагая число испытаний n=10, имеем оценку
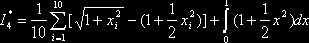 .
.
Выполнив элементарные преобразования, получим
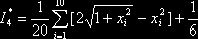 .
.
Учитывая, что a=0, b=1, возможные значения  разыграем по формуле
разыграем по формуле 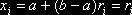 . Результаты вычислений приведены в таблице 4.
. Результаты вычислений приведены в таблице 4.

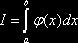 принимают
принимают 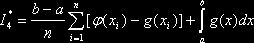 ,
, 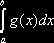 можно вычислить
обычными методами.
можно вычислить
обычными методами.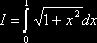 .
. 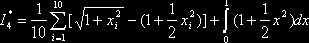 .
. Главная
Главная