Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9 | Следующая страница реферата

- ДПр - дополнительные преобразования;

- СО - статистическая обработка.

Имитационные системы имеют следующие функциональные блоки:

имитации входных процессов; имитации правил переработки входной информации исследуемой системы; накопления информации в результате моделирования; анализа накопленной информации; управления имитирующей системы.

Традиционный подход использует все классы задач, что и в методе Монте-Карло. Рассмотрим подробнее аналитический подход задания экзогенных переменных (первый случай). Они являются выходными другой подсистемы макросистемы и сами представляют собой макромодель. В рассматриваемом случае характеристики заданы аналитически.

Информационно технологическая блок-схема представлена на рис. 4.2.

Рис. 4.2. Технологический процесс имитационной системы

ГСП - генерирование случайных (входных) процессов;

ИС - имитационная система.

На первом этапе находят наиболее подходящие методы и алгоритмы для описания аналитических функций распределения и проводят вычисления (блок 1) для определения исходных данных, например, при аппроксимационных методах - координаты узлов, коэффициентов и т.п.

Во втором и третьем блоках производится генерирование случайных чисел с равномерным распределением x , и экзогенных случайных процессов z .

Блок 4 имитирует работу исследуемой системы, результаты его работы накапливаются для последующей статистической обработки. В последнем, пятом, блоке осуществляется статистическая обработка.

При моделировании систем на ЭВМ программная имитация случайных воздействий любой сложности сводится к генерированию некоторых стандартных (базовых) процессов и к их последующему функциональному преобразованию. В качестве базового может быть принят любой удобный в случае моделирования конкретной системы S процесс (например, пуассоновский поток при моделировании Q-схемы). Однако при дискретном моделировании базовым процессом является последовательность чисел 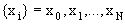, представляющих собой реализации независимых, равномерно распределенных на интервале (0,1) случайных величин 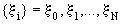или – в статистических терминах- повторную выборку из равномерно распределенной на (0,1) генеральной совокупности значений величины x .

Непрерывная случайная величина x имеет равномерное распределение в интервале (а,b), если ее функция плотности (рис. 4.3,а) и распределение (рис. 4.3,6) соответственно примут вид:

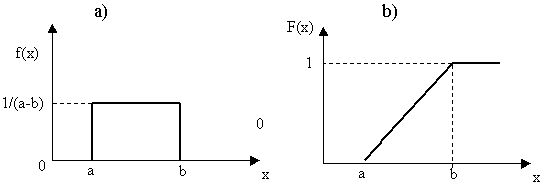
Рис. 4.3. Равномерное распределение случайной величины

2. Моделирование случайных величин и процессов

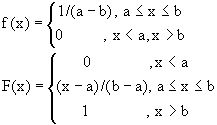
Под статистическим моделированием понимается воспроизведение с помощью ЭВМ функционирования вероятностной модели некоторого объекта.

Задачи статистического моделирования состоят в том, чтобы научиться воспроизводить с помощью ЭВМ поведение таких моделей, например:

с помощью специальных методов и средств вырабатывать программы реализации случайных чисел; с помощью этих чисел получать реализацию случайных величин или случайных процессов с более сложными законами распределения; с помощью полученных реализации вычислять значения величин, характеризующих модель, и производить обработку результатов экспериментов;

Устанавливать связь алгоритмов моделирования с алгоритмами решения задач вычислительной математики с помощью метода Монте-Карло и строить так называемые “фиктивные” модели, т.е. модели, не имеющие связи с объектом моделирования, но удобные в вычислительном отношении и позволяющие вычислять нужные нам характеристики объекта.

Моделирование случайных процессов строится на основе базовых распределений случайных величин.

Одним из таких процессов является марковские процессы.

3. Основные понятия марковских процессов

Марковские случайные процессы названы по имени выдающегося русского математика А.А. Маркова (1856-1922), впервые начавшего изучение вероятностной связи случайных величин и создавшего теорию, которую можно назвать “динамикой вероятностей”. В дальнейшем основы этой теории явились исходной базой общей теории случайных процессов, а также таких важных прикладных наук, как теория диффузионных процессов, теория надежности, теория массового обслуживания и т.д. В настоящее время теория марковских процессов и ее приложения широко применяются в самых различных областях таких наук, как механика, физика, химия и др.

Благодаря сравнительной простоте и наглядности математического аппарата, высокой достоверности и точности получаемых решений особое внимание марковские процессы приобрели у специалистов, занимающихся исследованием операций и теорией принятия оптимальных решений.

Несмотря на указанную выше простоту и наглядность, практическое применение теории марковских цепей требует знания некоторых терминов и основных положений, на которых следует остановиться перед изложением примеров.

Как указывалось, марковские случайные процессы относятся к частным случаям случайных процессов (СП). В свою очередь, случайные процессы основаны на понятии случайной функции (СФ).

Случайной функцией называется функция, значение которой при любом значении аргумента является случайной величиной (СВ). По- иному, СФ можно назвать функцию, которая при каждом испытании принимает какой-либо заранее неизвестный вид.

Рекомендуем скачать другие рефераты по теме: налоги в россии, бесплатные тесты бесплатно.





Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9 | Следующая страница реферата