Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9 | Следующая страница реферата

Вершины графа обозначают состояние , а дуги- переходные вероятности.

Множество состояний системы марковской цепи, определенным образом классифицируется с учетом дальнейшего поведения системы.

1. Невозвратное множество (рис. 3).

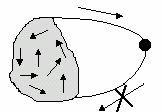
Рис. 3. Невозвратное множество

В случае невозвратного множества возможны любые переходы внутри этого множества. Система может покинуть это множество, но не может вернуться в него.

2. Возвратное множество (рис. 4).

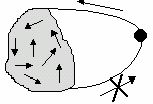
Рис. 4. Возвратное множество

В этом случае также возможны любые переходы внутри множества. Система может войти в это множество, но не может покинуть его.

3. Эргодическое множество (рис. 5).

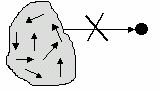
Рис. 5. Эргодическое множество

В случае эргодического множества возможны любые переходы внутри множества, но исключены переходы из множества и в него.

4. Поглощающее множество (рис. 6)

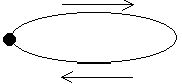
Рис. 6. Поглощающее множество

При попадании системы в это множество процесс заканчивается.

Кроме описанной выше классификации множеств различают состояния системы:

а) существенное состояние (рис.7): возможны переходы из 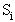в 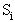и обратно.

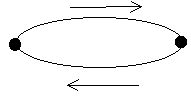
Рис. 7. Существенное состояние

б) несущественное состояние (рис. 8): возможен переход из 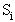в 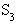, но невозможен обратный.

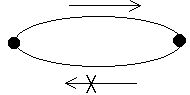
Рис. 8. Несущественное состояние

В некоторых случаях, несмотря на случайность процесса, имеется возможность до определенной степени управлять законами распределения или параметрами переходных вероятностей. Такие марковские цепи называются управляемыми. Очевидно, что с помощью управляемых цепей Маркова (УЦМ) особенно эффективным становится процесс принятия решений, о чем будет сказано впоследствии.

Основным признаком дискретной марковской цепи (ДМЦ) является детерминированность временных интервалов между отдельными шагами (этапами) процесса. Однако часто в реальных процессах это свойство не соблюдается и интервалы оказываются случайными с каким-либо законом распределения, хотя марковость процесса сохраняется. Такие случайные последовательности называются полумарковскими.

Кроме того, с учетом наличия и отсутствия тех или иных, упомянутых выше, множеств состояний марковские цепи могут быть поглощающими, если имеется хотя бы одно поглощающее состояние, или эргодическими, если переходные вероятности образуют эргодическое множество.

В свою очередь, эргодические цепи могут быть регулярными или циклическими. Циклические цепи отличаются от регулярных тем, что в процессе переходов через определенное количество шагов (циклов) происходит возврат в какое-либо состояние. Регулярные цепи этим свойством не обладают. Если просуммировать все вышесказанные определения, то можно дать следующую классификацию марковских процессов (рис. 9):

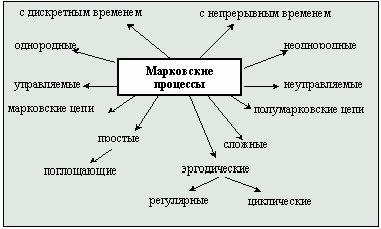
Рис. 9. Классификация марковских процессов

4. Математический аппарат дискретных марковских цепей

В дальнейшем рассматриваются простые однородные марковские цепи с дискретным временем. Основным математическим соотношением для ДМЦ является уравнение, с помощью которого определяется состояние системы на любом ее k-м шаге. Это уравнение имеет вид:

Рекомендуем скачать другие рефераты по теме: налоги в россии, бесплатные тесты бесплатно.





Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9 | Следующая страница реферата