Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9 | Следующая страница реферата

где .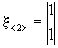

Для иллюстрации приведем конкретный числовой пример: пусть известны значения переходных вероятностей матрицы 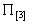с одним поглощающим состоянием: ; ; ; ; ; ; ; .

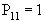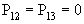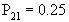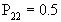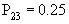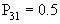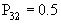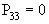Переходная матрица в блочной системе будет выглядеть так:

В данном случае

; ; ;

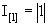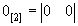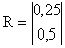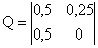
Проделаем необходимые вычисления:

;

;

.

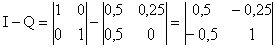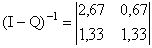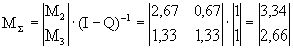В данном случае компоненты вектора 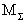означают, что если процесс начинается с состояния 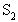, то общее среднее число шагов процесса до поглощения будет равно 3,34 и, соответственно, если процесс начинается с состояния 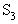, то - 2,26.

В конкретных задачах, конечно, более информативным результатом будет не количество шагов, а какие-либо временные или экономические показатели. Этот результат легко получить, если связать пребывание в каждом состоянии с соответствующими характеристиками. Очевидно, набор этих характеристик составит вектор, на который нужно умножить 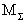слева.

Так, если задать в нашем примере время пребывания в состоянии 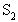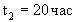, а в состоянии 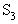- 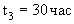, то общее время до поглощения будет равно:

В случаях, когда марковская цепь включает несколько поглощающих состояний, возникают такие вопросы: в какое из поглощающих состояний цепь попадет раньше (или позже); в каких из них процесс будет останавливаться чаще, а в каких - реже? Оказывается, ответ на эти вопросы легко получить, если снова воспользоваться фундаментальной матрицей.

Обозначим через 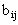вероятность того, что процесс завершится в некотором поглощающем состоянии 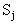при условии, что начальным было состояние 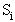. Множество состояний 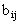снова образует матрицу, строки которой соответствуют невозвратным состояниям, а столбцы - всем поглощающим состояниям. В теории ДМЦ доказывается, что матрица В определяется следующим образом:

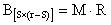(8.9)

где

М - фундаментальная матрица с размерностью S;

R - блок фундаментальной матрицы с размерностью r.

Рассмотрим конкретный пример системы с четырьмя состояниями 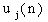, два из которых- 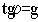- поглощающие, а два - 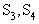- невозвратные (рис.10):

Рис. 8.10. Система с четырьмя состояниями

Для наглядности и простоты вычислений обозначим переходные вероятности следующим образом:

; ;

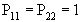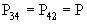
Остальные значения вероятностей будут нулевыми. Каноническая форма матрицы перехода в этом случае будет выглядеть так:

Рекомендуем скачать другие рефераты по теме: налоги в россии, бесплатные тесты бесплатно.





Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9 | Следующая страница реферата