Предыдущая страница реферата | 5  6  7  8  9  10  11  12  13  14  15 | Следующая страница реферата

При перепаде давлений между входным и выходным сечениями расчетной области 210-6 мм рт. ст. (около 410-4 Па) скорость ветра на верхней границе составила примерно 11 м/с, а на высоте, где обычно летают лыжники - около 5 м/с, что вполне согласуется с приведенными выше опытными данными.

Задача решалась при различных граничных условиях, что позволило выяснить, как влияет на расчет заданный перепад давлений или заданная входная скорость. Оказалось, что задав силовое граничное условие - перепад давлений - получаем такие скорости, что если задать их в качестве кинематических граничных условий, получается тот же перепад давлений, что и в первой задаче.

Из рисунка 9 видно, что во входном и в выходном участках области скорость ветра строго горизонтальна, а в районе горы имеет вертикальную составляющую, так как воздушный поток огибает гору. На рисунке 10, показывающем распределение поля давлений, видно, что давление над горой ниже, чем под горой, что и является причиной восходящего (огибающего гору) тока воздуха.

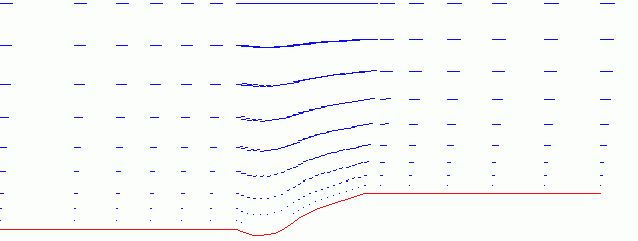
Рис.9

Поле скоростей ветра в окрестностях горы.

 

 

 

5. Расчет полета лыжника

Задача Коши (7),(14),(15),(8) решалась методом Гаусса решения систем дифференциальных уравнений.

Траекторию при заданных уравнениях движения и трамплине определяют три "входных" патаметра: начальная скорость , поддерживаемый в полете угол между лыжами и горизонталью и предельная скорость . После решения задачи Коши мы можем определить два "выходных" параметра задачи - составляющую посадочной скорости, нормальную к склону и дальность .

Далее для краткости будет называться просто скоростью приземления.

Исследовалась сходимость решения по интегральной и максимальной норме. Кроме этого проводилось еще две проверки, имеющих более простой и наглядный смысл. Их результаты здесь и приведены. Сравнение получающихся дальностей и скоростей приземления показало, что при заданном шаге по времени с дальность отличается по сравнению с решением с точностью с на величину порядка м, то есть у решений с шагами 0.001 с и 0.0001 с отличие в дальности имеет порядок нескольких миллиметров - в пределах одного сантиметра, т.е. 0.01 м. Численно отличие между скоростями приземления меньше в 2-3 раза, чем между дальностями. Так как точности выше 1 см и 1 см/с нам не нужны, все дальнейшие расчеты проводились с шагом по времени 0.001 с. Второй проверкой была такая: при отключении условия окончания вычислений по прошествии достаточно большого времени скорость падения становилась постоянной и равной предельной скорости. Оказалось, что значения выходных параметров достаточно жестко определяют, какими могут быть входные параметры. Это обусловлено не только узостью интервала допустимых скоростей приземления и длиной участка склона приземления, но и узостью интервалов изменения входных параметров. Вычислительный эксперимент проводился на параметрах нижне-тагильского трамплина. Входные параметры должны удовлетворять следующим условиям:

м/с

м/с

На рис.11 видны траектории полета прыгуна при , фиксированной предельной скорости и слегка отличающихся начальных скоростях.

Рис.11. Траектории полета лыжника при различных скоростях вылета

 

Рекомендуем скачать другие рефераты по теме: доклад на тему, класс.





Предыдущая страница реферата | 5  6  7  8  9  10  11  12  13  14  15 | Следующая страница реферата