Предыдущая страница реферата | 1  2  3  4  5  6 | Следующая страница реферата

Формулы Крамера.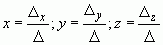

Метод Гаусса.

Пусть А - невырожденная матрица, то есть det A 0, и, следовательно, она имеет обратную матрицу А-1. Умножив обе части на А-1 слева, получаем:

А-1 (А Х) = А-1 В (А-1 А)Х = А-1 В Е Х = А-1 В, то есть Х = А-1 В и есть искомое решение системы (14). Действительно, подставив (16) в (14), получим А (А-1 В) = (А-1 А)В = Е В = В.

ТЕМА 7. Предел функции. ПОНЯТИЕ ФУНКЦИИ.

Если некоторому множеству значений 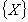поставлено по определенному правилу F во взаимнооднозначное соответствие некоторое множество 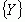, то тогда говорят, что на множестве 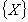определена функция 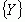. Множество 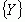называется областью изменения функции, множество 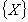– областью определения функции. Такая функция называется однозначной.

ЧИСЛОВАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ. ПРЕДЕЛ ЧИСЛОВОЙ ПОСЛЕДОВАТЕЛЬНОСТИ. ПРЕДЕЛ ФУНКЦИИ

Если некоторому множеству значений 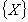поставлено по определенному правилу F несколько значений из множества 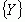, то тогда говорят, что на множестве 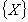задана многозначная функция.

Для того чтобы обозначить, что 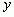есть функция от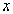, используют следующие виды записи: 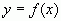;;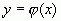 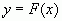и т.д.

Если невозможно выразить 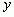, тогда говорят, что задана неявная функция и записывают: 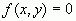;;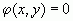 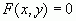и т.д.

Если надо выделить некоторое частное значение функции, соответствующее какому-либо конкретному значению 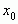, тогда записывают: .

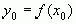Если каждому натуральному n по какому-либо известному правилу поставлено в соответствие некоторое число 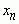, тогда говорят, что задана последовательность 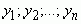, которая обозначается как 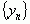Правило, по которому формируется последовательность 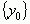, обозначается как 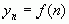и называется общим числом последовательности. Число 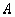назовем пределом последовательност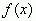и при 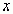стремящимся к 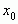, если для любого положительного, наперед заданного числа e , определяющего окрестность точки A, можно указать такую d , что для любого 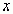, отличного от 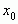из отрезка 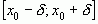значений функции 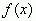принадлежит 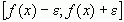и это записывают как .

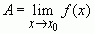Последовательность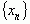называется бесконечно большой, если для любого числа 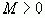найдется номер N, такой что для всех 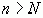выполняется неравенство 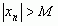. Геометрически это обозначает, что какой бы большой номер числа последовательности мы ни взяли, то всегда найдется число, принадлежащее этой последовательности, и лежащее правее выбранного, если последовательность составлена из положительных чисел, или левее, если последовательность составлена из отрицательных. Это записывают 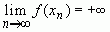, или .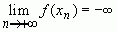

Последовательность 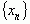называется бесконечно малой, если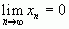

ТЕОРЕМА: Для того чтобы последовательность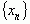сходилась к числу A необходимо и достаточно, чтобы выполнилось равенство 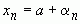, где .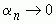

Эта теорема дает связь между пределом сходящейся последовательности и бесконечно малыми.

Функции 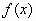называется непрерывной при 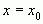или в точке 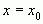, если выполняется 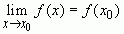.А так как функция при этом должна быть непрерывной в точке 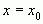, то должно быть справедливо .

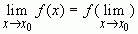Функция 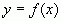называется непрерывной в точке 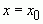, если для всех положительных, сколь угодно малых e можно указать такое положительное число 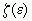, для которого выполняется неравенство 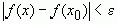для всех 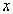из отрезка .

ТЕМА 8. Производная. ПРОИЗВОДНАЯ, ЕЁ СВОЙСТВА И ГЕОМЕТРИЧЕСКИЙ СМЫСЛ. ДИФФЕРЕНЦИАЛ. ПРОИЗВОДНАЯ ВЫСШИХ ПОРЯДКОВ

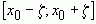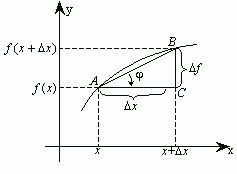
Если отношение 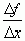имеет предел при 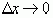этот предел называют производной функции 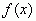при заданном значении 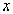и записывают .

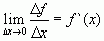Производная функции 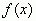в точке 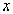численно равна тангенсу угла, который составляет касательная к графику этой функции построенной в точке 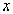с положительным направлением с осью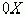

Из определения ясно - в случае убывающей функции производная отрицательна. Это объясняется тем, что 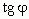, если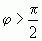будет отрицательным. На этом свойстве производной основано исследование поведения функции на возрастание (убывание) на заданном отрезке.

Производная алгебраической суммы равна алгебраической сумме производных. .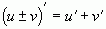

Производная произведения равна .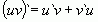

Если функция 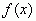имеет в точке 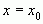производную 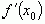и функция 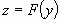имеет в точке 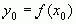производную 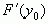, тогда сложная функция 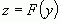имеет в точке 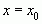производную, равную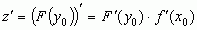

Если 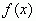имеет в точке 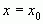производную, отличную от нуля, тогда в этой точке обратная функция 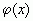также имеет производную и имеет место соотношение .

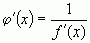Дифференцируя производную первого порядка, можно получить производную второго порядка, а, дифференцируя полученную функцию, получаем производную третьего порядка и т.д.

Пример 1. ; ; ; ...; ; .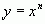

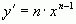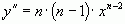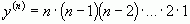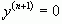Рекомендуем скачать другие рефераты по теме: шпора на пятке лечение, персонал реферат.





Предыдущая страница реферата | 1  2  3  4  5  6 | Следующая страница реферата