Предыдущая страница реферата | 1  2  3  4  5  6 | Следующая страница реферата

В последнем уравнении неизвестно b. Элементарным преобразованием из последнего уравнения получим

.

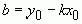Найденное b подставим в уравнение и окончательно

.

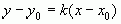Уравнение является уравнением прямой, проходящей через данную точку в заданном направлении.

УРАВНЕНИЕ ПРЯМОЙ ПО ДВУМ ТОЧКАМ

Неизвестен k - угловой коэффициент наклона линии по отношению к положительному направлению 0X. Однако, зная общий вид уравнения прямой (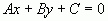 ) и учитывая, что обе точки расположены на искомой линии, можно составить следующую систему:

,

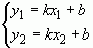где 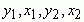– координаты точек M1 и M2 соответственно, (известны), а k и b – искомые неизвестные. Вычитая из первого уравнения второе, выразим k,

.

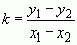Подставим найденное k в любое из уравнений и определим b

.

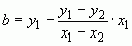Подставим найденные k и b в уравнение прямой

.

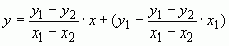Преобразуем последнее уравнение

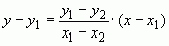
и окончательно

.

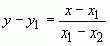Данное уравнение называется уравнением прямой, проходящей через две точки.

ТЕМА 5. Прямая и плоскость в пространстве. УРАВНЕНИЕ ПЛОСКОСТИ.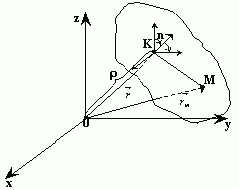

Любая поверхность есть геометрическое место точек, ее составляющих, определенное уравнением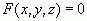

Иными словами, все точки, которые удовлетворяют этому уравнению, будут принадлежать поверхности.

Пусть в пространстве XYZ задана плоскость a и к ней в точке K проведем вектор нормали 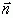. Так как плоскость a ориентирована произвольно в пространстве, то вектор 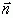будет составлять с осями x, y, z углы a , b и g соответственно.

Выберем на плоскости a точку M, не совпадающую с K и свяжем с этой точкой вектор 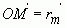. Очевидно, что 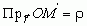, где r – модуль вектора 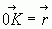, из уравнения получаем .

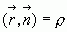Получаем нормальное уравнение плоскости: .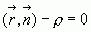

Однако, если представим вектор 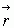как 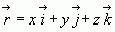, а вектор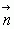 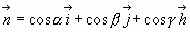, тогда подставив полученные выражения, получаем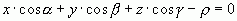

Зная, что для любой точки, принадлежащей плоскости, с координатами (A,B.C) можно вычислить направляющие косинусы

Рекомендуем скачать другие рефераты по теме: шпора на пятке лечение, персонал реферат.





Предыдущая страница реферата | 1  2  3  4  5  6 | Следующая страница реферата