Claw.ru | Рефераты по математике | О группах Ассура, фермах Баранова, цепях Грюблера, плоских шарнирных механизмах и об их структурном синт О группах Ассура, фермах Баранова, цепях Грюблера, плоских шарнирных механизмах и об их структурном синтезе | Категория реферата: Рефераты по математике | Теги реферата: понятие культуры, отчет о прохождении практики | Добавил(а) на сайт: Ярыкин. Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9 | Следующая страница реферата
Рис. 4

 

О девятизвенных фермах Баранова и их числе. В 1952 году Г.Г. Баранов синтезировал 26 таких ферм [7]. В 1971 году N.I. Manolescu и T. Erdelean [12] обнаружили две новых фермы, 27-ю и 28-ю, и доказали, что тем самым найдены все принципиально возможные девятизвенные статически определимые фермы с вращательными парами. Таким образом, общее число девятизвенных статически определимых ферм равно 28.

Авторы статьи [5], по-видимому, не знакомы с работой [12] (во всяком случае, в [5] на неё нет ссылки). На рис. 5 статьи [5] приведены 26 девятизвенных ферм Баранова [7], то есть не представлен полный состав таких ферм.

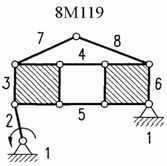
О восьмизвенных группах Ассура и их числе. Первое сообщение о числе восьмизвенных групп Ассура принадлежит И.И. Тартаковскому. В 1983 году в статье [13] он сообщил, что из 28 девятизвенных ферм Баранова можно получить 173 восьмизвенных группы Ассура (собственно группы Ассура в статье [13] не приводятся). В 1998 году группой авторов [2] синтезированы восьмизвенные группы, число которых тоже оказалось равным 173; причём, разработанный алгоритм синтеза не связан с использованием ферм Баранова. В качестве приложения к работе [2] был создан электронный каталог всех восьмизвенных групп Ассура.

Авторы статьи [5] утверждают (с. 35), что "в статье приведены все, построенные по найденным Барановым девятизвенным фермам группы Ассура". На рис. 7 статьи показаны 160 групп Ассура. Но при их построении не учтены 27-я и 28-я девятизвенные фермы [12], не обнаруженные самим Г.Г. Барановым. Кроме того, среди 160 групп имеется только 154 неповторяющихся группы, так как из ферм Баранова №№ 3, 4, 10, 14 и 15 (см. рис. 5 в статье [5]) можно получить соответственно 8, 5, 8, 8 и 8 восьмизвенных групп Ассура, а не 9, 6, 9, 9 и 9, как считают авторы статьи [5]; к тому же, группа №16-3 встречается на рис. 7 два раза. Помимо значения 160, в статье [5] дано ещё одно значение для числа групп: 167 (оно приведено на с. 31 в таблице 2, почему-то названной "Таблица Пейсаха Э.Е."). Но значение 167 никак не обосновано и нигде больше не встречается в статье [5].

Таким образом, в статье [5] приведены не все существующие восьмизвенные группы Ассура. Поэтому материалы этой статьи не дают оснований для пересмотра известного значения 173 для числа восьмизвенных групп.

О кинематических цепях Грюблера. Это понятие широко распространено в немецкоязычной и англоязычной литературе по теории механизмов (в публикациях на русском языке оно встречается довольно редко). В это понятие вкладывается вполне определённый смысл. Однако, авторы статьи [6] в ряде своих утверждений отклоняются от общепринятого толкования понятия "цепи Грюблера".

Например, они вводят понятие "неработоспособные цепи Грюблера" и довольно подробно его обсуждают. В частности, они приводят на рис. 8 "неработоспособную шестизвенную цепь Грюблера", а на рис. 9 две "неработоспособных восьмизвенных цепи Грюблера". Но те структуры, которые изображены на рисунках 8 и 9, вовсе не являются цепями Грюблера с 6 и 8 звеньями. Вообще, "неработоспособных" цепей Грюблера в принципе не существует. Далеко не любую систему из восьми твёрдых тел, соединённых десятью шарнирами, можно называть восьмизвенной цепью Грюблера. Так, "неработоспособная восьмизвенная цепь", показанная на рис. 9(а), есть в действительности четырёхзвенная кинематическая цепь, так как пять из восьми твёрдых тел представляют собою одно звено (эти пять тел, соединённых шарнирно, не имеют возможности перемещаться друг относительно друга).

Авторы статьи [6] считают, что "метод Грюблера по образованию механизмов может быть расширен. Из шестизвенных цепей Грюблера, оказывается, можно создавать не только шестизвенные механизмы, но и восьмизвенные. Для этого достаточно в каждую из цепей Грюблера вводить дополнительно по одному звену и по три шарнира". После этого авторы приводят ряд примеров, иллюстрирующих подобное "расширение" (см. рисунки 6 и 7). С таким расширительным толкованием метода Грюблера и цепей Грюблера никак нельзя согласиться. При образовании n-звенного механизма из n-звенной цепи Грюблера ничего дополнительно не вводится, а просто одно из звеньев цепи считается неподвижным (стойкой), а другое звено, смежное со стойкой, считается входным (или приводным).

По нашему мнению, при использовании понятия "цепи Грюблера" в литературе на русском языке лучше придерживаться общепринятого его толкования.

Список литературы

1. Woo L.S. Type Synthesis of Plane Linkages. – Transactions of ASME, Journal of Engineering for Industry, Vol. 89, 1967, p. 159-172.

2. Peisach E., Dresig H., Schönherr J., Gerlach S. Typ- und Masssynthese von ebenen Koppelgetrieben mit hoeheren Gliedgruppen (Zwischenbericht zum Fortsetzungsantrag) - DFG-Themennummer: Dr 234/7-1, TU Chemnitz, Professur Maschinendynamik / Schwingunglehre, Professur Getriebelehre, Chemnitz, 1998, 172 S.

3. Weinhold F. Zur rechnergestüzte Struktursynthese Kinematischer Ketten. – Doktor Thesis, Hannover, 1973.

4. Butcher E.A., Hartman C. Efficient enumeration and hierarchical classification of planar simple-jointed kinematic chains: Application to 12- and 14–bar single degree-of-freedom chains. – Mechanism and Machine Theory, Volume 40, No. 9, September 2005, p. 1030–1050.

5. Дворников Л.Т., Гудимова Л.Н. Анализ метода профессора Баранова Г.Г. по отысканию восьмизвенных плоских шарнирных групп Ассура. – Материалы шестнадцатой научно-практической конференции по проблемам механики и машиностроения / Под редакцией проф. Л.Т. Дворникова и проф. Э.Я. Живаго. – Сибирский государственный индустриальный университет, 2006, с. 27-40.

6. Дворников Л.Т., Фёдоров А.И. О сущности и возможностях метода М. Грюблера применительно к синтезу структур плоских механизмов. – Там же, с. 82-94.

7. Баранов Г.Г. Классификация, строение, кинематика и кинетостатика механизмов с парами первого рода. - Труды семинара по теории машин и механизмов, 1952, том 2, вып. 46, с. 15-39.

8. Пейсах Э.Е. К дискуссии по проблеме структурного синтеза плоских шарнирных механизмов. - Теория механизмов и машин. Научно-методический журнал. С.-Петербург: СПГТУ, 2006, № 1(7), том 4, с. 49-54. (Статья опубликована также в Internet'е на сайте: tmm.spbstu.ru).

9. Пейсах Э.Е. Атлас структурных схем восьмизвенных плоских шарнирных одноподвижных механизмов с входным звеном, присоединенным к стойке. - Сб.: Математика и механика. Часть Ш. Теоретическая и прикладная механика. - КазГУ, Алма-Ата, 1989, с. 163.

10. Пейсах Э.Е. Атлас структурных схем восьмизвенных плоских шарнирных механизмов. – Теория механизмов и машин. Научно-методический журнал. С.-Петербург: СПГТУ, 2006, № 1(7), том 4, с. 1-17. (Статья опубликована также в Internet'е на сайте: tmm.spbstu.ru).

Рекомендуем скачать другие рефераты по теме: конспекты по литературе, шпаргалки бесплатно.





Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9 | Следующая страница реферата