|
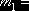 -0,7286 -0,7286
|
|
9
|
3,98119396
|
16
|
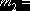 -0,6654 -0,6654
|
|
10
|
1,391261339
|
5
|
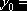 0,1632 0,1632
|
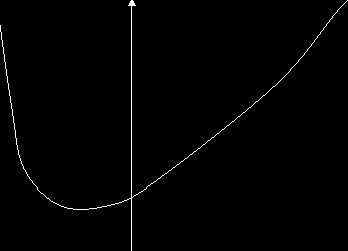
Кривая
распределения вероятностей имеет вид:
1

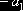 0
0 
Рис.
3
Такой
будет форма кривой распределения вероятностей, если параметры 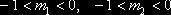 . Эта форма кривой встречается шестнадцать раз из пятидесяти.
. Эта форма кривой встречается шестнадцать раз из пятидесяти.
§2.
Алгоритм вычислений.




|
Тип кривой распределения вероятностей
|





|
Проверка условий для 
|









Метод Пирсона.
Заключение.
В
дипломной работе были рассмотрены вопросы нахождения распределения вероятностей
по заданным выборочным значениям случайной величины. В первой главе было
рассмотрено решение дифференциального уравнения Пирсона, проклассифицированы с
помощью æ критерия Пирсона, найдены типы кривых распределения
вероятностей и параметры, соответствующие каждому типу.
Во
второй главе был рассмотрен подход Чебышева к получению систем ортогональных
полиномов, которые обладают свойством метода наименьших квадратов. Было
рассмотрено применение способа Чебышева для нахождения кривой распределения
вероятностей по обобщенному методу Грамма – Шарлье.
В
третьей главе описывается алгоритмическое обеспечение нахождения кривых
распределения вероятностей по методу Пирсона.
Результаты
дипломной работы могут представлять большое значение для решения многих
практических задач, так как часто возникает необходимость по экспериментальным
данным оценить распределение вероятностей измеренной случайной величины.
Список литературы
Гмурман
В.Е. Теория вероятности и математическая статистика. Учебное пособие для вузов.
М.: Высшая школа, 1999
Джексон
Д. Ряды Фурье и ортогональные полиномы. М.: Государственное издательство
иностранной литературы, 1948
Митропольский
А.К. Техника статистических распределений. М.: издательство “Наука”, 1971
Немчинов
В.С. Полиномы Чебышева и математическая статистика. М.: издание Московской
ордена Ленина сельскохозяйственной академии имени К.А. Тимирязева, 1946
Романовский
В. И. Математическая статистика. Издательство Академии Наук УзССР, 1961
Суетин
П.К. Классические ортогональные многочлены. М.: издательство “Наука”, 1976
Хинчин
А. Я. Цепные дроби. М.: Государственное издательство физико-математической
литературы, 1961
Хотимский
В. И. Выравнивание статистических рядов по методу наименьших квадратов (способ
Чебышева). М.: Государственное статистическое издательство, 1959
Скачали данный реферат: Ikanov, Чкалов, Косарёв, Рыбяк, Jakimov, Ryzhanov.
Последние просмотренные рефераты на тему: организация диплом, контрольные 11 класс, лес реферат, реферат катастрофы.
Предыдущая страница реферата |
13
14
15
16
17
18
19
20
21
22
23

 Главная
Главная