Следовательно, кривая распределения вероятностей будет определена на промежутке 
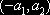 и будет иметь вид:
и будет иметь вид:

 1
1

 0
0 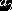
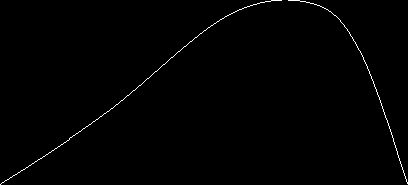
Рис.1
Из
чего следует, что если параметры кривой распределения первого типа будут
находиться в пределах  , то мы будем
получать форму кривой распределения, изображенную на рис.1.
, то мы будем
получать форму кривой распределения, изображенную на рис.1.
Из
пятидесяти рассмотренных выборок двадцать четыре имеют такую форму кривой
распределения вероятностей.
Пример
2.
Рассмотрим
другую выборку:
|

|
|
|
|
|
1
|
8,460199654
|
2
|
Кривая распределения вероятностей первого типа.
|
|
2
|
45,34087276
|
8
|
|
3
|
18,07745451
|
5
|
|
|
4
|
5,419406056
|
8
|
Параметры кривой:
|
|
5
|
18,67596108
|
6
|
|
|
6
|
23,24656701
|
9
|
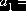 17,4066 17,4066
|
|
7
|
18,95143622
|
1
|
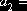 37,6794 37,6794
|
|
8
|
53,27426755
|
3
|
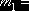 -0,3882 -0,3882
|
|
9
|
54,93095666
|
1
|
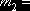 0,3243 0,3243
|
|
10
|
24,27284002
|
2
|
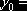 0,0187 0,0187
Рекомендуем скачать другие рефераты по теме: биология 6 класс, ответы 8 класс.
Предыдущая страница реферата | 13
14
15
16
17
18
19
20
21
22
23 | Следующая страница реферата
|
|

 1
1 Главная
Главная