
Принятие решений в условиях неопределенности
| Категория реферата: Рефераты по математике
| Теги реферата: налоги и налогообложение, легкие реферат
| Добавил(а) на сайт: Skuratov.
Предыдущая страница реферата | 1 2 3 4 5 6 7 8 9 10 11 | Следующая страница реферата
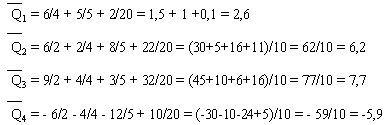
Максимальный средний ожидаемый доход равен 7.7, что соответствует 3-му решению.
Правило минимизации среднего ожидаемого риска. Риск фирмы при реализации i-го решения является случайной величиной Ri с рядом распределения
|
ri1 |
. . . |
rin |
|
p1 |
pn |
Математическое ожидание M[Ri] и есть средний ожидаемый риск, обозначаемый также Ri. Правило рекомендует принять решение, влекущее минимальный средний ожидаемый риск. Вычислим средние ожидаемые риски.

рj = ( 1/2 1/4 1/5 1/20 )
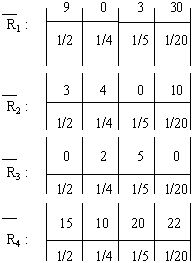
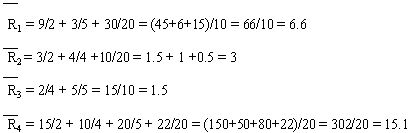
Минимальный средний ожидаемый риск равен 1.5, что соответствует 3-му решению.
Иногда в условиях полной неопределенности применяется следующее правило.
Правило Лапласа равновозможности, когда все вероятности p считаются равными. После этого можно выбрать какое-нибудь из двух приведенных выше правил-рекомендаций принятия решений.
Правило максимизации среднего ожидаемого дохода.

рj = ( 1/4 1/4 1/4 1/4 )
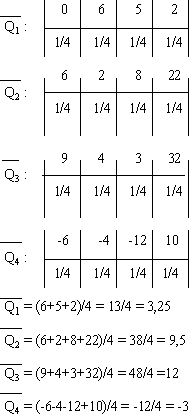
Максимальный средний ожидаемый доход равен 12, что соответствует 3-му решению.
Правило минимизации среднего ожидаемого риска.

рj = ( 1/2 1/4 1/5 1/20 )
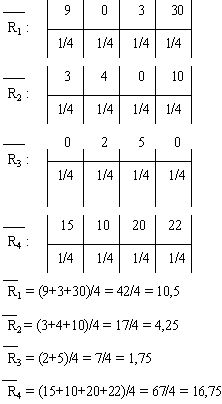
Минимальный средний ожидаемый риск равен 1.75, что соответствует 3-му решению.
При данных вероятностях состояний теперь требуется проанализировать семейство из 4-х операций: каждая операция имеет две характеристики — средний ожидаемый доход и средний ожидаемый риск. Точка (q’, r’) доминирует точку (q, r), если q’q и r’r. Точка, не доминируемая никакой другой, называется оптимальной по Парето.
Рекомендуем скачать другие рефераты по теме: 5 баллов, шпаргалки ответы.
Категории:
Предыдущая страница реферата | 1 2 3 4 5 6 7 8 9 10 11 | Следующая страница реферата
 Главная
Главная