Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9 | Следующая страница реферата

Далее числом 2 пометим точку, которой вместе с точкой O составляет пару, гармонически

сопряженную с парой (1, бесконечность). По известной теореме такую точку можно всегда построить и к тому же пара (O, 2) разделяет пару (1, бесконечность). Поэтому в линейном порядке т. 1 лежит между т. O и т. 2, или иначе, т. 2 следует за т. O и т. 1.

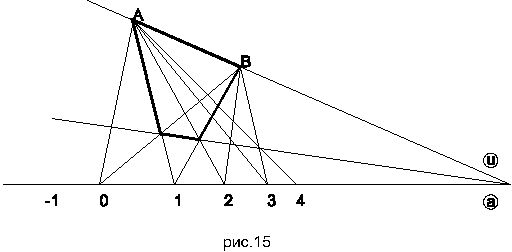
Построить т. 2 можно так: проведём через т. бесконечность прямой a две прямые, пометим их числом 1 и буквой U. Выберем на прямой u любую точку A. Проведём прямые AO и A1.

Они в пересечении с прямой 1 дадут точки (1, 0) и (1, 1). Далее проведём через т. O и (1, 1) прямую до пересечения с прямой u получим т. B. Соединим B и 1 и найдём точку пересечения прямой B1 и 1. Это точка (1,2). Проектируя эту точку на прямую a из центра A получим т. 2. Она и будет той четвёртой точкой в гармонически сопряжённых парах O, 2 и 1, бесконечность. Это можно показать, рассмотрев четырёхвершинник A, B, (1, 1), (1, 2).

Далее процесс построения аналогичный. Проектируя точку 2 на прямую 1 из т. B получим точку (1, 3). Проектируя последнюю на прямую a из точки A получим т.4 и т. д.

Аналогично можно получить точки, помеченные отрицательными числами. Так мы выстроили шкалу для определения целочисленных координат точек на прямой. Далее мы начинаем дробить отрезки и находить сначала координаты типа Z= (X+ Y)/2.

Оказывается, что точки Z, бесконечность составляют гармоническую пару с X, Y. Сама точка Z называется проективным центром отрезка (X, Y). Дробя далее отрезки можно присвоить каждой следующей дробной точке определённое число.

Таким образом, разрезанной проективной прямой получает соответствующее число, которое называют проективной координатой.

На проективной плоскости каждая точка получает две проективные координаты, в проективном пространстве- три.

До сих пор мы устраивали координатную систему на разрезанной проективной прямой, при этом одна точка, обозначаемая бесконечность, никакой координаты не получала.

Чтобы все точки получили значения, приходится употреблять "Однородные координаты".

Рассмотрим вначале систему однородных координат на проективной прямой а.

Отметим, что любая точка М этой прямой имеет некоторую координату х, введенную так, как показано в предыдущей лекции при задании системы координат точками 0,1, Ґ.При этом вполне определенную координату получает любая точка прямой, кроме точки Ґ.

Введем для точки М два числа х1 и х2, не равные одновременно нулю и такие, что их отношение (х1/х2)равно х. Эти числа (х1,х2) будем называть однородными координатами точки М. С точкой Ґ сопоставим однородные координаты х1, х2 при условии х2=0.

Свойства системы однородных координат: Каждая точка проективной прямой имеет однородные координаты. Если х1, х2 -однородные координаты т. М, то sх1, sх2, где s-любое число, отличное от нуля, есть тоже однородные координаты т. М. Разным точкам проективной прямой всегда соответствуют разные отношения их однородных координат.

Важнейшим свойством является второе: именно -каждая точка проективной прямой имеет бесконечно много пар однородных координат, которые сами по себе не определяются соответствующей им точкой, точка определяет лишь их отношение. Поэтому, подходящим подбором множителя s можно одну из координат взять равной единице (как правило -х2). Выпишем теперь однородные координаты базовых точек проективной прямой - точек 0, Ґ,1, обозначаемых А1 , А2 , А3 . А1 (0,1), А2 (1,0), А3 (1,1).

Однородные координаты па проективной плоскости

На проективной плоскости все точки, кроме лежащих на прямой Ґ (бесконечно удаленной прямой), имеют однородные проективные координаты. Базовыми точками для арифметизации проективной плоскости (т.е. введения проективных неоднородных координат) являются: начало системы координат О ; ҐХ (бесконечно удаленная на оси х), Ґy (бесконечно удаленная на оси y), (1,1) - единичная. Очевидно, бесконечно удаленная прямая проходит через точки Ґх и Ґy. Определим однородные проективные координаты сперва для точек проективной плоскости, не лежащих на прямой Ґ. Однородными координатами такой точки М назовем три числа х1 , х2 , х3 , не равных одновременно нулю и таких, что х1/х2=х; х2/х3=y, где х и y - проективные неоднородные (обычные) координаты. Однородными координатами точки МҐ , лежащей на прямой Ґ , назовем три числа х1 , х2 , х3 при условиях:

х3=0; Из двух чисел х1 , х2 хотя бы одно отлично от нуля; Отношение х1/х2 равно В/ (-А), где А и В - коэффициенты любой прямой Ах+Ву+С=0, проходящей через точку МҐ .

Если в уравнение прямой Ах+Ву+С=0 подставить однородные координаты некоторой точки М, лежащей на прямой (х=х1/х3, у=х2 /х3), то получим : Ах1+Вх2+Сх3=0, или иногда его записывают как:

u1 x1+u2 x2+u3 x3 = 0 - уравнение прямой в однородном виде (нет свободного члена)

Свойства однородных координат на плоскости:

1) Каждая точка проективной плоскости имеет однородные координаты

2) Если х1 , х2 , х3 - однородные координаты точки М, то s х1 , s х2 , s х3 (где s - любое отличное от нуля число) тоже являются однородными координатами точки М.

3) Разным точкам соответствуют разные отношения х1 / х3 , х2 / х3 их однородных координат.

Подходящим выбором s одну из координат можно сделать равной 1.Например, точка О - начало координат, получает однородные координаты (0,0,1), точка Ґх - (1, 0, 0), точка Ґу - (0,1,0), точка единиц по осям х и у - (1,1,1). Обозначим эти точки так: А1(1,0,0), А2(0,1,0), А3(0,0,1), Е(1,1,1) , их называют вершинами координатного триедра. Прямая А1 А2 - это бесконечно удаленная прямая - она имеет в однородных координатах уравнение х3 =0. Оси координат имеют свои обычные уравнения :

х1 =0, х2=0.

Однородные координаты в трехмерном пространстве.

Вводятся аналогично первым двум случаям. Сначала определим их для всех точек, не принадлежащих плоскости Ґ (бесконечно удаленной плоскости).

Однородными координатами таких точек называются любые четыре числа х1 , х2 , х3 , х4 , не равные одновременно нулю, и такие, что х1 /х4=х , х2 /х4=у, х3 /х4=z, где х, у, z - М. Если же точка М принадлежит плоскости Ґ , то ее однородные координаты определяются условиями : неоднородные (обычные) координаты точки:

Рекомендуем скачать другие рефераты по теме: реферат сфера, питание реферат.





Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9 | Следующая страница реферата