
Проективная геометрия
| Категория реферата: Рефераты по математике
| Теги реферата: недвижимость реферат, административное право шпаргалки
| Добавил(а) на сайт: Маркиана.
Предыдущая страница реферата | 1 2 3 4 5 6 7 8 9 | Следующая страница реферата
Элемент e называется единичным элементом.
4. Каким бы ни был элемент группы a, всегда существует такой элемент x, что ax=e.
Элемент x называется обратным элементу a и обозначается a-1, т. е. X= a-1.
Отсюда следуют такие правила:
a) если ax=e, то и xa=e
б) если e-единичный элемент группы, то ae= a и ea= a т. е. не различается "левая" и "правая" единицы
в) из соотношения ax= e обратный элемент x определяется однозначно
Если все эти положения применить к проективным преобразованиям, а именно к представляющим их матрицам проективных преобразований в однородных координатах, то можно сказать, что совокупность проективных преобразований составляет группу:
1) произведение двух проективных матриц есть вновь матрица проективного преобразования;
2) (c1c2)c3= c1(c2c3)
3) единичный элемент

4) условием существования обратного элемента является условие существования обратной матрицы, для последнего необходимо, чтобы [c]#0 это условие является требованием проективного преобразования.
Группу проективных преобразований называют проективной группой.
Прежде чем рассмотреть матрицы проективных преобразований, соответствующих конкретным их типам, вспомним иерархию геометрических преобразований.

Для однозначного определения матрицы преобразования 1го уровня необходимо (n+2) точки. Для однозначного определения матрицы преобразования 2го уровня необходимо (n+1) точка. Для однозначного определения матрицы преобразования 3го уровня необходимо n точек.
 Матрицы конкретных проективных преобразований.
Матрицы конкретных проективных преобразований.
Каждое преобразование более низкого уровня является одновременно и преобразованием более высокого
1) На плоскости. Перенос на вектор n (a,b)
P/=M(n )P P, P/ - однородные координаты
Поворот на угол j против часовой стрелки вокруг начала координат.
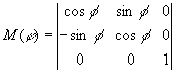
Маштабирование относительно начала координат.
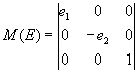 неоднородное
неоднородное
2) В пространстве
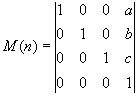
Рекомендуем скачать другие рефераты по теме: реферат сфера, питание реферат.
Категории:
Предыдущая страница реферата | 1 2 3 4 5 6 7 8 9 | Следующая страница реферата
 Главная
Главная