Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9 | Следующая страница реферата

Это означает, что при инволюционном отображении число неподвижных точек не может быть больше 2.Дискреминант уравнения (3) есть a2+bg =-D.

Если -D<0, (дискриминант отрицательный), то уравнение (3) не имеет действительных корней, то есть нет ни одной неподвижной точки. Такая инволюция называется эллиптической (ее условие --a2-bg >0).

Если - D >0, то есть D<0 , -a2-bg <0 , то уравнение (3) имеет два действительных корня или две неподвижные точки- называется такая инволюция гиперболической.

Если D =0, то есть -a2-bg =0 , параболическая инволюция, но в этом случае такое отображение не входят в группу проективных преобразований, так как оно не взаимно однозначно.

Существует теорема , что для однозначного определения инволюции надо задать две пары соответствующих точек на прямой, в отличии от общих формул проективного отображения прямой на прямую, где надо задать три пары точек.

Следующий инвариант проективной геометрии - сложное отношение четырех точек на прямой.

Оно определяется так :Пусть М1,М2,M3,M4-четыре точки некоторой проективной прямой. Введем систему проективных неоднородных координат , и обозначим через t1,,t2,t3,t4, координаты заданных точек. Можно показать, что величина (t3-t1)/(t2-t3):(t4-t1)/(t2--t4 )

не зависит от выбора координатной системы, а определяется только положением точек на прямой.

Эта величина обозначается (М1 М2 M3 M4)= (t3-t1)/(t2-t3):(t4-t1)/(t2--t4 ) и называется сложным отношением четырех точек (СОЧТ).

Непосредственным вычислением можно показать, что выполняются два свойства СОЧТ.

1) (М1 М2 M3 M4)=(M3M4M1M2)

2) (М1 М2 M3 M4)= 1/ (М1 М2 M3 M4) то есть СОЧТ не меняется при перестановке первой и второй пар точек , изменяется на обратную величину при перестановке точек внутри какой-нибудь пары.

Важная теорема проективной геометрии гласит.

При любом проективном отображении прямой а на прямую а/ сложное отношение произвольной группы точек М1 М2 М3 М4 прямой а равно сложному отношению соответствующих им точек М1/ M2/ M3/ M4/ прямой а/ .

Частным ее случаем является утверждение:

В плоскости a заданы две прямые а и а/ ,задана произвольная точка S ,принадлежащая плоскости a ,но не лежащая на прямых а и а/. Тогда, сложное отношение любой четверки точек М1 М2 М3 М4 прямой а равно сложному отношению их проекций М1/М2/ М3/ М4/ из центра S на прямую а/ .

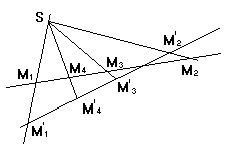
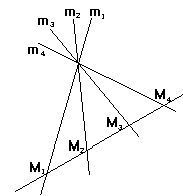
Аналогичное утверждение можносформулировать для плоского пучка из четырех лучей m1 m2 m3 m4

Любая прямая, пересекающаяэти четыре луча в

четырех точках, имеет для этих четырех точек одно и тоже сложное отношение.

(М1 М2 М3 М4)=инвариант проективной геометрии

или, что тоже самое (m1 m2 m3 m4 ) - инвариант проективной геометрии

Основной вывод : Сложное отношение четырех элементов одномерного многообразия - есть инвариант проективных отображений. Можно показать, что если пара точек А ,В гармонически разделяет пару точек С,D, то сочетание (А В С D)=-1.Оно вытекает из свойства гармонического сопряжения , когда каждая точка первой пары делит отрезок, образуемый второй парой точек внутренним и внешним образом в одинаковом отношении

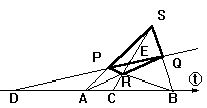
АС/AD=BC/BD или через неоднородные координаты ti точек (1,2,3,4) соответствует ( A , B , C , D )

(t3 - t1)/(t1 - t4) = (t2 - t3)/(t2 - t4) или (t3 - t1)/(t2 - t3) =

- (t4 - t1)/(t2 - t4) или ((t3 - t1)/(t2 - t3))/((t4 - t1)/(t2 - t4))=-1

Рекомендуем скачать другие рефераты по теме: реферат сфера, питание реферат.





Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9 | Следующая страница реферата