Предыдущая страница реферата | 9  10  11  12  13  14  15  16  17  18  19 | Следующая страница реферата



Если целое число, равное числу изменений знака, обозначить через V(b), то число собственных значений в интервале действительных чисел [b, с] будет равно V(b)—V(c).

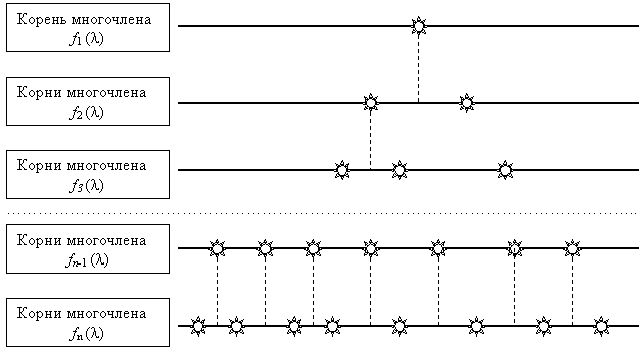
Рис. 3. Итерационное определение корней полинома

6. ДРУГИЕ МЕТОДЫ ВЫЧИСЛЕНИЯ СОБСТВЕННЫХ ЗНАЧЕНИЙ

В этом разделе мы рассмотрим два метода определения собственных значений, имеющие большое практическое значение. Оба разработаны в последние 20 лет и наиболее эффективны в тех случаях, когда требуется найти все собственные значения произвольной матрицы действительных или комплексных чисел. В обоих используются преобразования, позволяющие получить последовательность подобных матриц, сходящуюся к матрице блочной треугольной формы:

X1	*		…	…	*	*	*
	x2	*	…	…	*	*	*
		x3	…	…	*	*	*
			…	…	*	*	*
				…	*	*	*
					…	*	*
	0					…	*
							*

где блоки Хm, представляют собой матрицы размерности 2 х 2, расположенные на главной диагонали. Собственные значения блоков Хm, являются в то же время собственными значениями исходной матрицы размерности п x п. Такая форма удобна, так как детерминант второго порядка блоков Хm позволяет определять комплексные собственные значения, не вводя комплексных элементов в окончательную матрицу. Если все собственные значения исходной матрицы действительные, то в окончательном виде она будет треугольной, причем собственные значения будут расположены на диагонали.

Метод LR

Этот метод первоначально был разработан Рутисхаузером в 1958 г. Метод основан на представлении матрицы A в виде произведения

А = LR,

где L — левая треугольная матрица с единичными диагональными элементами, а R — правая треугольная. Применяя преобразование подобия L-1 A R, видим, что,

Рекомендуем скачать другие рефераты по теме: доклади по биологии, рефераты по политологии.

Предыдущая страница реферата | 9  10  11  12  13  14  15  16  17  18  19 | Следующая страница реферата