Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата

Индусы рассматривали числа безотносительно к геометрии. В этом их алгебра имеет сходство с алгеброй Диофанта. Они распространили правила действия над рациональными числами на числа иррациональные, производя над ними непосредственные выкладки, а не прибегая к построениям, как это делали греки. Например, им было известно, что

Греки, не знавшие отрицательных чисел, решая уравнения, преобразовывали их так, чтобы обе части уравнения при значении неизвестной, удовлетворяющей этому уравнению, были положительными. Если этого не происходило, то менялись условия задачи. Индусы в аналогичных ситуациях не были стеснены в своих действиях: они либо отбрасывали получающиеся отрицательные решения, либо интерпретировали их как долг, задолженность. Отсюда сделан был естественный шаг к установлению правил действий над величинами при любом выборе знаков этих величин, а также к выявлению наличия двух корней у квадратных уравнений и двузначности квадратного корня.

Индусами был сделан шаг вперед по сравнению с Диофантом и в совершенствовании алгебраической символики: они ввели обозначения нескольких различных неизвестных и их степеней, которые были, как у Диофанта, по сути дела сокращениями слов. Кроме того, они искали решения неопределенных уравнений не в рациональных, а в целых числах.

2.1.4 Алгебра арабов.

Дальнейшее развитие математика получила у арабов, завоевавших в VII в. Переднюю Азию, Северную Африку и Испанию. Создались благоприятные условия для слияния двух культур – восточной и западной, для усвоения арабами богатого математического наследия эллинов и индусской арифметики и алгебры.

Но еще до того как началось усиленное изучение арабами трудов древних математиков, в 820 г., вышел трактат по алгебре «Краткая книга об исчислении ал-джабра и ал-мукабалы» Мухаммеда ибн Муса ал-Хорезми (т. е. из Хорезма, 787 – ок. 850г. н. э.), где давались числовое и геометрическое решения уравнений первой и второй степеней.

 Название трактата соответствует операциям при решении уравнений: «ал-джабр» (восстанавливать) означает восстановление отрицательного члена в одной части уравнения в виде положительного в другой. Например, преобразовав уравнение

2х2 + Зх -2 = 2х к виду 2х2 + Зх = 2х + 2, мы произвели операцию ал-джабр.

 «Ал-мукабала» означает сопоставление подобных членов, приведение их к одному; в нашем уравнении подобные члены Зх и 2х, поэтому получим 2x2 + x = 2.

Модификация слова ал-джабр породила более позднее алгебра. Аналогично, слово алгорифм (алгоритм) произошло от ал-Хорезми.

Основное внимание в трактате ал-Хорезми обращает на решение уравнений вида

ax2 = bx, ax2 = c, ax2 + bx = c, ax2 + c = bx, bx + c = ax2, bx = c,

которые формулирует словесно, например, так: «квадраты и корни равны числу» (ах2 + bх = с). Он высказывает правила, дающие только положительные решения уравнений, определяет условия, при которых эти решения существуют. Обоснование правил ал-Хорезми дает в духе геометрической алгебры древних.

От арабов Европа получила следующий способ решения уравнения

х2 + ах = b.

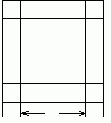
Построим квадрат х2, к его сторонам приложим четырехугольники длины х + 2а/4 = х + а/2 и ширины а/4. Тогда площадь полученного квадрата = x2 + ax + .

Значит, x2 + ax +  = = b + , = b + .

Величины b и а известны, поэтому можно построить , откуда х + = -. Впрочем, ал-Хорезми, приведший в своем сочинении этот метод, уравнению ах2 + с = bх приписывал два корня.

В трактате приведены некоторые сведения о действиях над алгебраическими выражениями, примеры решения треугольников много задач о разделе наследства приводящих к уравнениям первой степени. Таким образом, трактат ал-Хорезми не содержал ничего нового по сравнению с тем, что было у греческих авторов и индусов, но он заслуживает внимания потому, что в течение длительного времени был руководством, по которому велось обучение в Европе.

2.1.5 Развитие алгебры в Европе.

Каково же было состояние математики в это время в Европе. Об этом наука располагает крайне скудными сведениями.

В XII – XIII вв. в Европе интенсивно переводились в арабского языка как труды самих арабов, так и работы древних греков, переведенные на арабский язык.

Первым европейским математиком, которому удалось осветить многие вопросы и внести в математику свой вклад, был Леонардо Пизанский (Фибоначчи, 1180–1240), написавший «Книгу абака». В ней рассмотрены различные задачи, указаны методы их решения, причем арифметика и алгебра линейных и квадратных уравнений изложены с небывалой до этого времени точностью и полнотой.

Существо задачи Леонардо излагает словесно; неизвестную он называет res (вещь) или radix (корень); квадрат неизвестной – census (имущество) или quadratus (квадрат); данное число – numerus. Все это латинские пероводы соответствующих латинских слов.

Современник Леонардо, Иордан Неморарий (XIII в), употреблял буквенные обозначения более систематично и решал задачи с применением линейных и квадратных уравнений, сначала в общем виде, а затем иллюстрировал их числовыми примерами.

Рекомендуем скачать другие рефераты по теме: образ сочинение, реферат бесплатно без регистрации.





Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата