Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата

Выведем теперь ее.

Рассмотрим уравнение х3 + px + q = 0. Введем новые неизвестные x = u + v и подставим их в исходное уравнение; получим u3 + v3 + (3uv + p)(u + v) + q = 0.

Приравняем 3uv + p к нулю: 3uv + p = 0.

Уравнение примет вид u3 + v3 + q = 0. Тогда uv = – , u3v3 = – , u3 + v3 = -q.

Выражения u3 и v3 можно принять за корни квадратного уравнения z2 + qz – = 0.

Решая его, получим z1 = –  + , z2= – – .

Таким образом, x = u + v = +, x =+.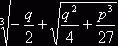

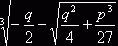Это и есть формула Кардано. Не лишне заметить, что в таком виде Кардано ее не искал: он формулировал решение уравнений (1)и (2) и рассматривал связь между уравнениями (2) и (3).

В случае, когда +0.

Для получения уравнения четвертой степени возведем левую и правую части уравнения в квадрат:

(х2 + ах - b)3 = x4 + a2x2 + b2 + 2ax3 – 2bx2 – 2abx = 0

Полученное уравнение можно переписать:

x4 + 2ах3 + 2а2x2 – а2x2+ b2 – 2bх2 – 2abx = 0.

Исключим 2ах3 + 2a2x2, воспользовавшись тем, что b = х2 + ax:

2ах(х2 + аx) = b2аx, 2ах3 + 2a2x = 2abx.

Тогда x4 + 2abx – а2x2 + b2 – 2bx2 – 2abx = 0, x4 – a2x2 + b2 – 2bx2 = 0.

Теперь осталось исключить x2; из исходного уравнения найдем: x2 = b – ax и подставим в последнее:

 x4 – (a2 + 2b)x2 + b2 = 0, x4 – (a2 + 2b)(b – ax) + b2 = 0, x4 + (2ab + a3)x = b2 + a2b

Полученное уравнение четвертой степени имеет те и только те положительные корни, которые были у исходного квадратного.

Для нахождения трехчленного уравнения третьей степени Виет в качестве исходного брал уравнение

ax – x2 = ab

и умножал его левую и правую части на х + b; это при водило к уравнению

(а – b)х2 – х3 = ab2

с теми же положительными корнями, которые были у квадратного.

И еще один частный вопрос рассмотрел Виет. В уравнении

Рекомендуем скачать другие рефераты по теме: образ сочинение, реферат бесплатно без регистрации.





Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата