Claw.ru | Рефераты по математике | Солнечный ветер Солнечный ветер | Категория реферата: Рефераты по математике | Теги реферата: форма реферата, пример дипломной работы | Добавил(а) на сайт: Бурда. Предыдущая страница реферата | 1  2  3  4  5  6  7  8 | Следующая страница реферата

Решение 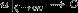также удовлетворяет уравнению (8). В этом случае первый и третий члены в левой части уравнения (9) стремятся к нулю и

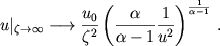
(9б)

Таким образом, решение уравнения (8) на больших расстояниях имеет две ветви: верхнюю () и нижнюю (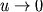). Для того чтобы выбрать решение, приемлемое с физической точки зрения, вычислим плотность плазмы, соответствующую этим решениям.

Из равенства (4) следует

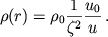
(10)

Подставляя в (10) величину из (9а), (9б), находим

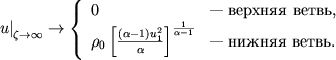
(11)

Из равенств (11) видно, что в случае, когда 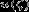соответствует нижней ветви решения, плотность плазмы при 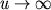стремится к конечной и относительно большой величине, что противоречит экспериментальным данным. В то же время верхняя ветвь решения соответствует 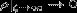, что удовлетворяет условиям модели. Таким образом, на больших расстояниях от Солнца физический смысл имеет лишь верхняя ветвь решения уравнения Паркера.

Малые расстояния ()

При третий член в левой части равенства (8) неограниченно возрастает. Поскольку в правой части уравнения постоянная величина, это означает, что неограниченное возрастание 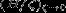должно быть скомпенсировано одним из первых двух членов в левой части (8), то есть опять имеют место две ветви решения:

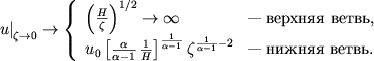
(12)

Первое решение, соответствующее неограниченному возрастанию скорости солнечного ветра при , физически неприемлемо. Второе решение дает разумный результат 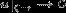при значениях показателя политропы, определяемых неравенством 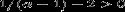, то есть .

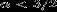Таким образом, стационарное решение короны оказывается возможным лишь в том случае, если показатель политропы a меньше адиабатического (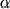 = 5/3), то есть если имеет место непрерывный приток энергии в корону и солнечный ветер. В первоначальной модели Паркера предполагалось, что необходимый приток энергии обеспечивается высокой теплопроводностью солнечной плазмы. Однако, как будет показано ниже, одного лишь потока тепловой энергии недостаточно для ускорения солнечного ветра, и требуются дополнительные источники энергии.

Итак, мы видим, что физически разумным граничным условиям при больших удовлетворяет верхняя ветвь решения уравнения Паркера, а при малых - нижняя. Сращивание этих двух ветвей решения зависит от поведения решения в окрестностях некоторой критической точки, положение которой на плоскости 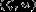определяется следующим образом.

Продифференцируем уравнение (8) по :

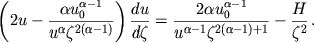
(13)

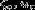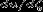Определим критическую точку () как точку, где правая часть уравнения (13) и коэффициент при в левой части уравнения одновременно равны нулю. Тогда

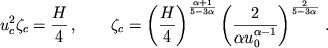
(14)

Топология решения уравнения (8) в окрестностях критической точки показана на рис. 1. Решение представляет собой семейство гипербол. При этом существует лишь одно решение, удовлетворяющее граничным условиям как на больших, так и на малых расстояниях от Солнца. Этому решению соответствует кривая, проходящая через критическую точку (критическое решение).

Рекомендуем скачать другие рефераты по теме: реферат образ жизни, реферат по русскому языку.





Предыдущая страница реферата | 1  2  3  4  5  6  7  8 | Следующая страница реферата