Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата

Теорема: Для любого ограниченного оператора А, действующего из нормированного пространства в нормированное,

= .

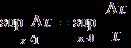Определение: Пусть А и В – два линейных оператора, действующих из линейного топологического пространства Е в пространство Е1. Назовём суммой А+В оператор С, ставящий в соответствие элементу хЕ элемент

y=Ax+ByE1.

С=А+В – линейный оператор, непрерывный, если А и В непрерывны. Область определения Dc есть пересечение DADB областей определения оператора А и оператора В.

Если Е и Е1 – нормированные пространства, а операторы А и В ограничены, то С тоже ограничен, причём

.

Это следует из:

.

Определение: Пусть А и В – линейные операторы, причём А действует из пространства Е в Е1, а В действует из Е1 в Е2. Произведением ВА операторов А и В называется оператор, ставящий в соответствие элементу хЕ элемент

z=B(Ax)

из Е2. Область определения DC оператора С=ВА состоит из тех хDA, для которых AxDB. Ясно, что оператор С линеен. Он непрерывен, если А и В непрерывны.

Если А и В – ограниченные операторы, действующие в нормированных пространствах, то и оператор С=ВА ограничен, причём

Это следует из:

Обратный оператор. Обратимость

Пусть А – оператор, действующий из Е в Е1, и DA – область определения, а RA – область значений этого оператора.

Определение: Оператор А называется обратимым, если для любого  уравнение

имеет единственное решение.

Если А обратим, то каждому  можно поставить в соответствие единственный элемент , являющийся решением уравнения . Оператор, осуществляющий это соответствие, называется оператором обратным к А и обозначается .

Рассмотрим оператор, переводящий конечномерное пространство в конечномерное. Выше было сказано, что он задаётся матрицей коэффициентов. Таким образом, оператор обратим, если обратима матрица коэффициентов, которой он задаётся. А матрица обратима лишь в том случае, если её определитель не равен нулю. То есть матрицы, которые имеют ненулевой определитель, задают обратимый оператор, переводящий конечномерное пространство в конечномерное.

Теорема: Оператор , обратный к линейному оператору А, также линеен.

Теорема Баноха об обратном операторе: Пусть А – линейный ограниченный оператор, взаимно однозначно отображающий банахово пространство Е на банахово пространство Е1. Тогда обратный оператор  тоже ограничен.

Рекомендуем скачать другие рефераты по теме: правовые рефераты, задачи с ответами.





Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата