Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата

тогда . Видно, что резольвента существует и непрерывна, когда существует и непрерывен интеграл.

Резольвентное множество. Спектр

Пусть А – оператор, действующий в В-пространстве. Если  регулярна, т.е. оператор  существует и ограничен, то при достаточно малом  оператор  тоже существует и ограничен, т.е. точка + тоже регулярна. Таким образом, регулярные точки образуют открытое множество. Докажем это.

Теорема: Резольвентное множество  открыто, функция резолвента  аналитична в этой области.

Доказательство:

Пусть  - фиксированная точка в  и  - любое комплексное число, такое, что . Покажем, что . Оператор  должен иметь обратный, если . Этот обратный оператор, если он существует, будет выглядеть так:

.

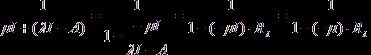Рассмотрим эту дробь как сумму бесконечно убывающей геометрической прогрессии, тогда она представима в виде ряда

.

Мы предполагали, что , то , следовательно, этот ряд сходится. Покажем, то  это резольвента :

,

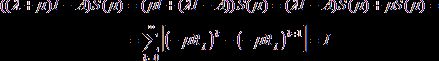отсюда и следует, что  и что = аналитична в точке

Доказано.

Следовательно, спектр, т.е. дополнение этого множества – замкнутое множество, и резольвента аналитична на бесконечности.

Следствие: Если  равно расстоянию от  до спектра , то

, .

Таким образом,  при  и резольвентное множество есть естественная область аналитичности .

Доказательство:

В доказательстве предыдущей теоремы мы видели, что если , то . Следовательно, , от куда и следует доказываемое утверждение.

Доказано.

Резольвента как функция от

А сейчас рассмотрим резольвенту как функцию от и докажем несколько утверждений о её свойствах и особенностях. Для доказательства следующего утверждения нам понадобится следующая теорема.

Теорема 5: Пусть Е – банахово пространство, I – тождественный оператор в Е, а А – такой ограниченный линейный оператор, отображающий Е в себя, что . Тогда оператор  существует, ограничен и представляется в виде

.

Доказательство:

Рекомендуем скачать другие рефераты по теме: правовые рефераты, задачи с ответами.





Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата