Claw.ru | Рефераты по математике | Теория массового обслуживания с ожиданием Теория массового обслуживания с ожиданием | Категория реферата: Рефераты по математике | Теги реферата: персонал диплом, зимой сочинение | Добавил(а) на сайт: Соболев. Предыдущая страница реферата | 1  2  3  4  5  6  7  8 | Следующая страница реферата при t£0, при t>0,

2. Составление уравнений.

система с ожиданием в случае простейшего потока и показательного времени обслуживания представляют собой случайный процесс Маркова.

Найдём те уравнения, которым удовлетворяют вероятности Pk(t). Одно из уравнений очевидно, а именно для каждого t

.                                                   (2)

Найдем сначала вероятность того, что в момент t+h все приборы свободны. Это может произойти следующими способами:

  в момент t все приборы были свободны и за время h новых требований не поступало;

  в момент t один прибор был занят обслуживанием требования, все остальные приборы свободны; за время h обслуживание требования было завершено и новых требований не поступило.

Остальные возможности, как-то: были заняты два или три прибора и за время h работа на них была закончена - имеют вероятность o(h), как легко в этом убедится.

Вероятность первого из указанных событий равна

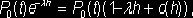
вероятность второго события

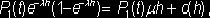
Таким образом,

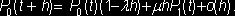
Отсюда очевидным образом приходим к уравнению

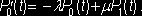                                   (3)

Перейдем теперь к составлению уравнений для Pk(t) при k ³ 1. Рассмотрим отдельно два различных случая: 1 £ k < m и k ³ m. Пусть вначале 1 £ k < m. Перечислим только существенные состояния, из которых можно прийти в состояние Ek в момент t+h. Эти состояния таковы:

В момент t система находилась в состоянии Ek, за время h новых требований не поступило и ни один прибор не окончил обслуживания. Вероятность этого события равна

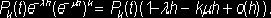
В момент t система находилась в состоянии Ek-1, за время h поступило новое требование, но ни одно ранее находившееся требование не было закончено обслуживанием. Вероятность этого события равна

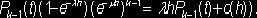
В момент t система находилась в состоянии Ek+1 , за время h новых требований не поступило, но одно требование было обслужено. Вероятность этого равна

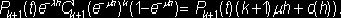
Рекомендуем скачать другие рефераты по теме: 1 ответ, рефераты баллы.





Предыдущая страница реферата | 1  2  3  4  5  6  7  8 | Следующая страница реферата