Предыдущая страница реферата | 1  2  3  4  5  6  7  8 | Следующая страница реферата

kmPk=lPk-1    (10)

и при k ³ m   mmPk=lPk-1    (11)

Введем для удобства записи обозначение

r=l/m.

Уравнение (10) позволяет заключить,  что при  1 £ k < m

    (12)

При k ³ m из уравнения (11) находим, что

и следовательно,  при k ³ m

   (13)

Остается найти P0. Для этого в (9) подставляем выражения Pk из (12) и (13). В результате

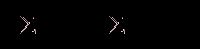
Так бесконечная сумма, стоящая в квадратных скобках, находится только при условии, что

r < m      (14)

то при этом положении находим равенство

   (15)

Если условие (14) не выполнено,  т.е. если r ³ m, то ряд,  стоящий в квадратной скобке уравнения для определения P0 , расходится и, значит, P0 должно быть равно 0. Но при этом, как следует из (12) и (13), при всех k ³ 1 оказывается Pk =0.

Методы теории цепей Маркова позволяют заключить, что при r ³ m с течением времени очередь стремится к ¥ по вероятности.

4. Некоторые подготовительные результаты.

Во введении мы уже говорили, что для задачи с ожиданием основной характеристикой качества обслуживания является длительность ожидания требованием начала обслуживания. Длительность ожидания представляет собой случайную величину, которую обозначим буквой g. Рассмотрим сейчас только задачу определения распределения вероятностей длительности ожидания в уже установившемся процессе обслуживания. Обозначим далее через P{g > t} вероятность того, что  длительность ожидания превзойдет t, и через Pk{g > t} вероятность неравенства, указанного в скобке, при условии, что в момент поступления требования, в очереди уже находится k требований. В силу формулы полной вероятности имеем равенство

P{g > t}=.    (16)

Прежде чем преобразовать эту формулу к виду, удобному для пользования, приготовим некоторые необходимые нам для дальнейшего сведения. Прежде всего  для случаев m=1 и m=2 найдем простые формулы для P0. несложные преобразования приводят к таким равенствам: при m=1

P0=1-r,     (17)

а при m=2

     (18)

Рекомендуем скачать другие рефераты по теме: 1 ответ, рефераты баллы.





Предыдущая страница реферата | 1  2  3  4  5  6  7  8 | Следующая страница реферата