Предыдущая страница реферата | 1  2  3  4  5 | Следующая страница реферата

Точно так же показывается, что при трехкратном бросании вероятность невыпадения 6 составляет

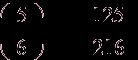
А при четырехкратном –

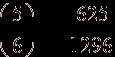
А , следовательно, вероятность выигрыша . Значит, при каждой игре больше половины шансов было за то, что де Мере выиграет; при многократном повторении игры он наверняка оставался в выигрыше.

Резонно поставить вопрос, какой должна быть вероятность события, чтобы можно было считать его достоверным? Известно, что примерно 5% назначенных концертов отменяется, однако это не мешает нам покупать билеты. Но если бы 5% самолетов разбивались, то вряд ли бы кто-нибудь стал пользоваться воздушным транспортом.

Для того, чтобы в условиях мирного времени не рисковать жизнью, то вероятность неблагоприятного исхода должна быть, по-видимому, не больше 0,0001. Разные люди по-разному относятся к риску, но очевидно, что даже самые осторожные легко пойдут на риск, если вероятность неблагоприятного исхода составляет 10-5. Например, вероятность попасть под машину в большом городе 10-7. Так что можно предположить, что событие с вероятностью неблагоприятного исхода 10-7 можно считать достоверным, однако транспортные происшествия случаются каждый день.

Так же можно определить вероятность невозможного события, например «чуда Бореля» (Эмиль Борель – математик, автор многих работ по Теории) – того, что обезьяна, наугад ударяя пальцами по клавиатуре, напечатает какое-нибудь законченное произведение, например, «Горе от ума» Грибоедова. Это не невозможное событие, хотя вероятность его очень мала, примерно 10-2600. С такой же вероятностью на огне может замерзнуть чайник (термодинамика, кстати, не отрицает возможности такого явления).

Но все-таки вероятность невозможного события большинство ученых оценивает как 10-16.

4. Метод «Монте-Карло».

определение. Метод Монте-Карло – это численный метод решения математических задач при помощи моделирования случайных величин.

Датой рождения метода принято считать 1949 г., когда появилась в свет статья «The Monte Carlo Method». Создатели метода – американские математики Дж. Неймана и С. Улама.

Теоретическая основа метода была известно давно, однако только с появлением компьютеров он нашел широкое применение, т.к. моделировать случайные величины вручную – трудоемкое занятие.

Само название метода – «Монте-Карло» происходит от названия города в княжестве Монако, знаменитого своими игорными домами. Дело в том, что простейшим прибором для моделирования случайных величин является… рулетка. Наиболее часто задаваемый вопрос, естественно: «Помогает ли метод выигрывать в рулетку». Нет, к сожалению, не помогает.

Теперь перейдем непосредственно к математике. Чтобы было понятно, о чем идет речь, приведем простейший пример применения метода.

Пример 1.

Предположим, нам надо вычислить площадь фигуры, изображенной на рисунке. Предположим, что она расположена внутри единичного квадрата.

Выберем внутри единичного квадрата N случайных точек. Обозначим через N’ число точек, попавших внутрь этой фигуры. Тогда площадь этой фигуры будет приближенно равна .

На рисунке всего 30 точек. 12 из них попали в фигуру,  , в то время как истинная площадь фигуры равна 0,48.

Особенности Метода.

Первая особенность – простота вычислительного алгоритма. Как правило, составляется программа для проведения одного случайного испытания, и повторять его N раз. Поэтому Метод часто называют методом статистических испытаний

Вторая особенность – погрешность, как правило, пропорциональна , где D = const, N – число испытаний.

Разные задачи можно решать разными вариантами Метода, которых, кстати, очень много. Для каждого варианта – свое значение D и, соответственно, свое значение погрешности.

С помощью Метода можно смоделировать любой процесс, протекание которого связано со случайными величинами. Так же можно искусственно придумать вероятностную модель для задач, не связанных со случайностью.

Для получения случайных чисел существуют специальные таблицы, которыми особенно удобно пользоваться на компьютерах: каждый раз мы просто берем очередное число и используем его как случайное. Но составить такую таблицу не так просто, как может показаться. Существуют специальные тесты, чтобы проверить правильность случайной последовательности.

Практическое значение Метода очень велико. С его помощью, например, можно рассчитать надежность любого изделия, или рассчитать траекторию прохождения нейтронов сквозь пластину или положение электрона в данный момент времени и т.д.

Рекомендуем скачать другие рефераты по теме: доклады 7 класс, конспект.





Предыдущая страница реферата | 1  2  3  4  5 | Следующая страница реферата