Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата



Пусть W состоит из конечного числа элементарных событий W={E1, E2,..., Em} тогда по определению . Элементарные события несовместны, тогда по третей аксиоме теории вероятности имеет место

Пусть некоторое событие AÌW состоит из k элементарных событий, тогда {Ei1, Ei2,..., Eik}

Доказать: Если AÌB, то P(B)³P(A), B=A+C, A и  C несовместны.

* Пусть B=A+C, A и B несовместны. Тогда по третей аксиоме теории вероятности P(B)=P(A+C)=P(A)+P(C)  т.к. 1³P(C)³0 - положительное число, то P(B)³P(A).

Классическое определение вероятности.

Пусть W состоит из конечного числа элементарных событий и все элементарные события равновероятны, т.е. ни одному из них из них нельзя отдать предпочтения до испытания, следовательно, их можно считать равновероятными.

Тогда достоверное событие   m - количество равновероятных событий

,                  ,             

Пусть произвольное событие  Тогда , т.е. событие A состоит из k элементарных событий.

Если элементарные события являются равноправными, а, следовательно, и равновероятными, то вероятность наступления произвольного события равна дроби числитель которой равен числу элементарных событий, входящих в данное, а знаменатель - общее число элементарных событий.

Условная вероятность.

P(A/B)

Условной вероятностью наступления события A, при условии события B, называется вероятность наступления события A в результате испытаний, если известно, что в это испытании произошло событие B.

Вывод формулы условной вероятности для случая равновероятных элементарных событий

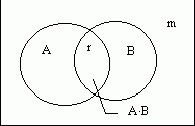
Действительно, в данном испытании произошло одно из t событий, входящих в B. Все элементарные события равновероятны, следовательно, для данного испытания вероятность наступления произвольного элементарного события, входящего в B равна 1/t. Тогда по классическому определению вероятности, в данном испытании событие A произойдет с вероятностью r/t.

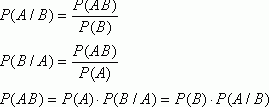
В общем случае доказать эту формулировку невозможно, в теории вероятности она вводится как правило. Существует лишь толкование этой формулы.

Обоснование формулы условной вероятности в общем случае.

Пусть в nB испытаниях произошло событие B, а в nA испытаниях произошло событие A. Найдем условную частость наступления события A при условии, что произошло событие B. Мы можем сделать это для обоснования формулы, т.к. под вероятностью наступления события понимается предел частости наступления события при условии, что серия испытаний достаточно длинная.

Условная частость

Рассматривая AB как одно событие D имеем:  с другой стороны

Рассмотрим систему событий A1, A2,...,Ak. Покажем, что вероятность их совместного наступления равна:    

Рекомендуем скачать другие рефераты по теме: quality assurance design patterns системный анализ, 5 баллов рефераты.

Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата