Выбор в качестве х минимального среди чисел, стоящих в
отрицательных вершинах цикла, обеспечивает допустимость нового базиса.
Если минимальное значение среди базисных неизвестных, стоящих в отрицательных вершинах цикла, принимается не в одной отрицательной
вершине, то свободной оставляют только одну из них, а в других клетках с тем же
минимальным значением пишут нули. В этом случае новое базисное решение будет
вырожденным.
Может случиться, что и само минимальное значение среди
чисел в отрицательных клетках равно нулю. Тогда преобразование таблицы
перевозок сведется к перестановке этого нуля в свободную клетку. Значения всех
неизвестных при этом остаются неизменными, но решения считаются различными, так
как различны базисы. Оба решения вырождены.
Описанное выше преобразование таблицы перевозок, в
результате которого преобразуется базис, называется пересчетом по циклу.
Заметим, что неизвестные, не входящие в цикл, этим
преобразованием не затрагиваются, их значения остаются неизменными и каждое из
них остается либо в группе базисных, либо в группе свободных неизвестных, как
и до пересчета.
Выясним теперь, как пересчет по циклу влияет на общий
объем затрат на перевозки и при каком условии эти затраты становятся меньше.
Пусть 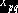 – некоторое свободное
неизвестное, для которого мы построили цикл и осуществили пересчет по циклу с
некоторым числом
– некоторое свободное
неизвестное, для которого мы построили цикл и осуществили пересчет по циклу с
некоторым числом  . Если вершине цикла, находящейся в
. Если вершине цикла, находящейся в  строке и
строке и 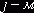 столбце таблицы
перевозок, приписан знак “+”, то значение неизвестного
столбце таблицы
перевозок, приписан знак “+”, то значение неизвестного 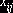 , находящегося в этой вершине, увеличивается на
, находящегося в этой вершине, увеличивается на  , что в свою очередь вызывает увеличение затрат на
, что в свою очередь вызывает увеличение затрат на 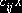 . где
. где 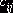 – тариф, соответствующий этой клетке; если же указанной вершине приписан знак “–”, то
значение неизвестного
– тариф, соответствующий этой клетке; если же указанной вершине приписан знак “–”, то
значение неизвестного 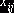 уменьшается на
уменьшается на  , что вызывает уменьшение затрат на
, что вызывает уменьшение затрат на 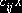 .
.
Сложим тарифы, соответствующие положительным вершинам
цикла, и вычтем из этой суммы сумму тарифов, соответствующих отрицательным
вершинам цикла; полученную разность 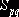 назовем алгебраической
суммой тарифов для данного свободного неизвестного
назовем алгебраической
суммой тарифов для данного свободного неизвестного 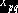 . Подсчет алгебраической суммы тарифов можно истолковать и
так: припишем тарифам те же знаки, которые приписаны соответствующим вершинам
цикла, тогда алгебраическая сумма тарифов равна сумме таких тарифов со знаком
(“относительных тарифов”).
. Подсчет алгебраической суммы тарифов можно истолковать и
так: припишем тарифам те же знаки, которые приписаны соответствующим вершинам
цикла, тогда алгебраическая сумма тарифов равна сумме таких тарифов со знаком
(“относительных тарифов”).
Теперь, очевидно, мы можем, заключить, что в целом при
пересчете но циклу, соответствующему свободному неизвестному 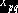 общий объем затрат на
перевозки изменится на произведение алгебраической суммы тарифов на
общий объем затрат на
перевозки изменится на произведение алгебраической суммы тарифов на  , т. е. на величину
, т. е. на величину 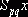 . Следовательно, если алгебраическая сумма тарифов для
некоторого свободного неизвестного
. Следовательно, если алгебраическая сумма тарифов для
некоторого свободного неизвестного 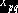 отрицательна
отрицательна 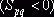 , то пересчет по циклу, соответствующему этому неизвестному, приводит к уменьшению общей суммы затрат на реализацию плана перевозок. Если же
алгебраическая сумма тарифов положительна
, то пересчет по циклу, соответствующему этому неизвестному, приводит к уменьшению общей суммы затрат на реализацию плана перевозок. Если же
алгебраическая сумма тарифов положительна 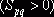 , то пересчет по соответствующему циклу приведет к увеличению
общей суммы затрат. И, наконец, если алгебраическая сумма тарифов равна нулю
, то пересчет по соответствующему циклу приведет к увеличению
общей суммы затрат. И, наконец, если алгебраическая сумма тарифов равна нулю 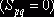 , то пересчет по соответствующему циклу не изменит общую
сумму затрат (два различных базисных плана требуют одинаковых затрат на их
реализацию).
, то пересчет по соответствующему циклу не изменит общую
сумму затрат (два различных базисных плана требуют одинаковых затрат на их
реализацию).
Так, например, для цикла 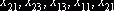 в рассмотренной задаче
алгебраическая сумма тарифов
в рассмотренной задаче
алгебраическая сумма тарифов
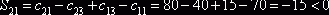 .
.
Значит, пересчет по этому циклу снижает расходы. И
действительно, осуществив такой пересчет, мы получаем план, по которому объем
перевозок в тонно-километрах составляет
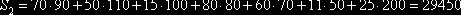
тогда как по исходному плану он составил 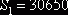 . Имеем снижение объема перевозок на 1200 тонно-километров, что и следовало ожидать, так как алгебраическая сумма тарифов в данном случае
равна –15, а пересчет по циклу осуществляется с помощью числа
. Имеем снижение объема перевозок на 1200 тонно-километров, что и следовало ожидать, так как алгебраическая сумма тарифов в данном случае
равна –15, а пересчет по циклу осуществляется с помощью числа 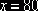 (изменение затрат
равно
(изменение затрат
равно 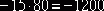 ).
).
Вычисление алгебраической суммы тарифов для каждого из
свободных неизвестных можно производить без построения соответствующего
цикла, пользуясь, так называемыми, потенциалами. Припишем каждой базе 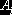 , некоторое число
, некоторое число 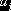 и каждому потребителю
и каждому потребителю 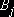 некоторое число
некоторое число 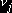 :
:
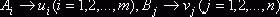 ,
,
так что
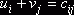
,
где 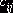 – тарифы, соответствующие клеткам, заполненным базисными неизвестными. Эти числа
– тарифы, соответствующие клеткам, заполненным базисными неизвестными. Эти числа 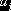 и
и 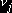 называются
потенциалами соответствующих баз и потребителей.
называются
потенциалами соответствующих баз и потребителей.
Зная потенциалы, легко вычислить алгебраическую сумму
тарифов. Действительно, если в алгебраической сумме тарифов по циклу, соответствующему свободному неизвестному 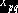 , заменить тарифы базисных клеток их выражениями через
потенциалы по формулам (4.1), то, в силу чередования знаков при вершинах цикла, все потенциалы, кроме
, заменить тарифы базисных клеток их выражениями через
потенциалы по формулам (4.1), то, в силу чередования знаков при вершинах цикла, все потенциалы, кроме 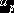 и
и 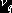 сократятся, и мы
получим:
сократятся, и мы
получим:
Рекомендуем скачать другие рефераты по теме: сайт рефератов, контрольная работа 7.
Предыдущая страница реферата |
9
10
11
12
13
14
15
16
17
18
19 |
Следующая страница реферата

 Главная
Главная