Claw.ru | Рефераты по математике | Транспортная задача линейного программирования Транспортная задача линейного программирования | Категория реферата: Рефераты по математике | Теги реферата: сочинение описание, курсовики скачать бесплатно | Добавил(а) на сайт: Эсмеральда. Предыдущая страница реферата | 6  7  8  9  10  11  12  13  14  15  16 | Следующая страница реферата		120	20
Потребности	170	110	100	120	200	700

В данном случае заполнение таблицы начинается с клетки для неизвестного 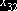, для которого мы имеем значение 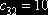, наименьше из всех значений . Эта клетка находится на пересечении третьей строки и второго столбца, соответствующим третьей базе 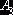 и второму заказчику 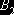. Третья база  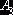может полностью удовлетворить потребность второго заказчика 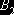 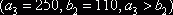. Полагая 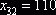, вписываем это значение в клетку  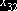и исключаем из рассмотрения второй столбец. На базе 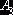 остается изменённый запас 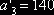. В оставшейся новой таблице с тремя строками  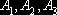и четырьмя столбцами  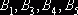клеткой с наименьшим значением  клетка, где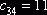. Заполняем описанным выше способом эту клетку и аналогично заполняем следующие клетки. В результате оказываются заполненными (в приведенной последовательности) следующие клетки:

.

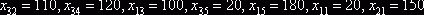На пятом шаге клеток с наименьшими значениями 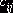 оказалось две 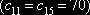. Мы заполнили клетку для 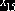, положив 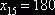. Можно было выбрать для заполнения другую клетку, положив 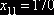, что приведет в результате к другому опорному плану. Общий объем перевозок в тонно-километрах для этого плана составит

.

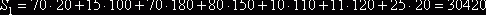Замечание. В диагональном методе не учитываются величины тарифов, в методе же наименьшей стоимости эти величины учитываются, и часто последний метод приводит к плану с меньшими общими затратами (что и имеет место в нашем примере), хотя это и не обязательно.

Кроме рассмотренных выше способов иногда используется, так называемый, метод Фогеля. Суть его состоит в следующем: В распределительной таблице по строкам и столбцам определяется разность между двумя наименьшими тарифами. Отмечается наибольшая разность. Далее в строке (столбце) с наибольшей разностью заполняется клетка с наименьшим тарифом. Строки (столбцы) с нулевым остатком груза в дальнейшем в расчет не принимаются. На каждом этапе загружается только одна клетка. Распределение груза производится, как и ранее.

4.Понятие потенциала и цикла.

Для перехода от одного базиса к другому при решении транспортной задачи используются так называемые циклы.

Циклом пересчета или короче, циклом в таблице перевозок называется последовательность неизвестных, удовлетворяющая следующим условиям:

Одно из неизвестных последовательности свободное, а все остальные – базисные.

Каждые два соседних в последовательности неизвестных лежат либо в одном столбце, либо в одной строке.

Три последовательных неизвестных не могут находиться в одном столбце или в одной строке.

Если, начиная с какого-либо неизвестного, мы будем последовательно переходить от одного к следующему за ним неизвестному то, через несколько шагов мы вернемся к исходному неизвестному.

Второе условие означает, что у двух соседних неизвестных в цикле либо первые, либо вторые индексы одинаковы.

Если каждые два соседних неизвестных цикла соединить отрезком прямой, то будет получено геометрическое изображение цикла – замкнутая ломаная из чередующихся горизонтальных и вертикальных звеньев, одна из вершин которой находится в свободной клетке, а остальные - в базисных клетках.

Можно доказать, что для любой свободной клетки таблицы перевозок существует один и только один цикл, содержащий свободное неизвестное из этой клетки, и что число вершин в цикле всегда четно.

Так, например, в таблице перевозок, составленной по диагональному методу при решения задачи из предыдущего пункта, неизвестному 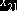 соответствует цикл  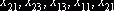и т.д.

Рекомендуем скачать другие рефераты по теме: сайт рефератов, контрольная работа 7.





Предыдущая страница реферата | 6  7  8  9  10  11  12  13  14  15  16 | Следующая страница реферата