Предыдущая страница реферата | 11  12  13  14  15  16  17  18  19  20  21 | Следующая страница реферата

Отсюда вытекает способ отыскания оптимального решения транспортной задачи, состоящий в том, что, имея некоторое базисное решение, вычисляют алгебраические суммы тарифов для всех свободных клеток. Если критерий оптимальности выполнен, то данное решение является оптимальным; если же имеются клетки с отрицательными алгебраическими суммами тарифов, то переходят к новому базису, производя пересчет по циклу, соответствующему одной из таких клеток. Полученное таким образом новое базисное решение будет лучше исходного – затраты на его реализацию будут меньшими. Для нового решения также проверяют выполнимость критерия оптимальности и в случае необходимости снова совершают пересчет по циклу для одной из клеток с отрицательной алгебраической суммой тарифов и т. д.

Через конечное число шагов приходят к искомому оптимальному базисному решению.

В случае если алгебраические суммы тарифов для всех свободных клеток положительны, мы имеем единственное оптимальное решение; если же алгебраические суммы тарифов для всех свободных клеток неотрицательны, но среди них имеются алгебраические суммы тарифов, равные нулю, то оптимальное решение не единственное: при пересчете по циклу для клетки с нулевой алгебраической суммой тарифов мы получим оптимальное же решение, но отличное от исходного (затраты по обоим планам будут одинаковыми).

В зависимости от методов подсчета алгебраических сумм тарифов для свободных клеток различают два метода отыскания оптимального решения транспортной задачи:

Распределительный метод. При этом методе для каждой пустой клетки строят цикл и для каждого цикла непосредственно вычисляют алгебраическую сумму тарифов.

Метод потенциалов. При этом методе предварительно находят потенциалы баз и потребителей, а затем вычисляют для каждой пустой клетки алгебраическую сумму тарифов с помощью потенциалов.

Преимущества метода потенциалов по сравнению с распределительным методом состоят в том, что отпадает необходимость построения циклов для каждой из пустых клеток и упрощается вычисление алгебраических сумм тарифов. Цикл строится только один – тот, по которому производится пересчет.

Применяя метод потенциалов, можно говорить не о знаке алгебраических сумм тарифов, а о сравнении косвенных тарифов с истинными. Требование неотрицательности алгебраических сумм тарифов заменяется условием, что косвенные тарифы не превосходят истинных.

Следует иметь в виду, что потенциалы (так же как и циклы) для каждого нового базисного плана определяются заново.

Выше рассматривалась закрытая модель транспортной задачи, с правильным балансом, когда выполняется условие (1.3). В случае выполнения (1.4) (открытая модель) баланс транспортной задачи может нарушаться в 2-ух направлениях:

1. Сумма запасов в пунктах отправления превышает сумму поданных заявок (транспортная задача с избытком запасов):

 å аi > å bj ( где i=1,...,m ; j=1,...,n );

2. Сумма поданных заявок превышает наличные запасы (транспортная задача с избытком заявок): 

 å аi < å bj ( где i=1,...,m ; j=1,...,n );

Рассмотрим последовательно эти два случая:

Транспортная задача с избытком запасов.

Сведем её к ранее рассмотренной транспортной задаче с правильным балансом. Для этого, сверх имеющихся n пунктов назначения В1, B2, ... , Bn, введём ещё один, фиктивный, пункт назначения Bn+1, которому припишем фиктивную заявку, равную избытку запасов над заявками 

 bn+1 = å аi - å bj ( где i=1,...,m ; j=1,...,n ) ,

а стоимость перевозок из всех пунктов отправления в фиктивный пункт назначения bn+1 будем считать равной нулю. Введением фиктивного пункта назначения B n+1 с его заявкой b n+1 мы сравняли баланс транспортной задачи, и теперь ее можно решать, как обычную транспортную задачу с правильным балансом.

Транспортная задача с избытком заявок.

Эту задачу можно свести к обычной транспортной задаче с правильным балансом, если ввести фиктивный пункт отправления Am+1 с запасом am+1 равным недостающему запасу, и стоимость перевозок из фиктивного пункта отправления во все пункты назначения принять равной нулю.

Задача, двойственная к транспортной.

Построим задачу, двойственную к транспортной. С этой целью вспомним, что каждому пункту отправления  и назначения  отвечает определенное ограничение

(6.1)

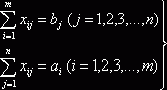
Рекомендуем скачать другие рефераты по теме: сайт рефератов, контрольная работа 7.





Предыдущая страница реферата | 11  12  13  14  15  16  17  18  19  20  21 | Следующая страница реферата