Предыдущая страница реферата | 1  2  3  4  5  6  7 | Следующая страница реферата

где  при .

Тогда имеет место следующее равенство:

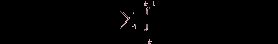                               (1.19)

при , где  - оператор Штурма-Лиувилля задачи (1.1)-(1.3), а  - оператор задачи (1.4)-(1.6). Из (1.18) и (1.19) нетрудно показать справедливость оценки (1.14). Теорема доказана.

Следствие 1.1 ,

.

Следствие 1.2 , где  - характеристическое уравнение для собственных значений задачи (1.4)-(1.6),  - характеристическое уравнение для собственных значений задачи (1.1)-(1.3).

Следствие 1.3  и совпадают со всеми корнями уравнения .

Следствие 1.4  образуют полную систему собственных функций.

II. Сингулярная задача. Случай .

Будем рассматривать задачу

,                                     (2.1)

,                                     (2.2)

где  монотонно, т.е. уравнение (2.1) имеет не более одной точки поворота. Таким образом, для любого . В случае, когда , спектральная задача имеет дискретный спектр. Из представленного метода решения регулярной задачи следует, что ; таким образом, для каждого  задачи на полуоси ставится в соответствие своя регулярная задача на конечном отрезке . Если бы мы знали все значения собственных функций , соответствующие собственным числам задачи на полуоси, в точке , то, решая задачи на конечном промежутке  с дополнительным граничным условием , мы могли бы вычислить все собственные числа задачи на  достаточно точно. Исходя из сказанного, можно утверждать, что погрешность определения собственных чисел тем меньше, чем точнее выбор второго краевого условия. В связи с этим рассмотрим два краевых условия  (условие Дирихле) и  (условие Неймана). Пусть  - собственные числа задач на конечном промежутке с дополнительными условиями Дирихле и Неймана соответственно. С помощью метода решения регулярной задачи доказываются следующие утверждения:

ТЕОРЕМА 2.1 Справедлива асимптотическая формула собственных чисел задачи на полуоси

,                                         (2.3)

где [1] .

Справедливость теоремы 2.1 следует из следствия 1.1.

ТЕОРЕМА 2.2 Справедливо неравенство:

.                                                        (2.4)

Доказательство теоремы 2.2 можно провести с помощью функций распределения собственных чисел (см. [2]) или с помощью метода, предложенного в первой части работы, и следствия 1.1.

Замечание В случае полуограниченного оператора (), данный выбор краевых условий позволяет получать лишь верхнюю и нижнюю оценку собственных чисел.

Следствие 2.1 , где  - длина промежутка .

Пример

.

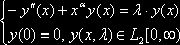Рекомендуем скачать другие рефераты по теме: конспект урока в школе, дипломы рефераты.





Предыдущая страница реферата | 1  2  3  4  5  6  7 | Следующая страница реферата