Вычисление собственных чисел и собственных функций опрератора Штурма-Лиувилля на полуоси

| Категория реферата: Рефераты по математике
| Теги реферата: страна реферат, скачать на телефон шпаргалки
| Добавил(а) на сайт: Яновицкий.

 при  монотонно, и , где ;

 при , .

Данная задача рассматривалась в работе Е.ПЖидкова. и А.Г.Соловьева (см. [5]). Известно, что задача имеет собственные числа и собственные функции такие, что все ее собственные числа простые, отрицательные и образуют бесконечно возрастающюю последовательность  с единственной предельной точкой , а собственные функции , отвечающие собственным значениям , имеют в интервале  в точности  нулей. В этом случае справедливы все результаты, полученные для случая полуограниченного оператора.

Пример

 .

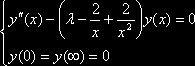Известно (см. [3]), что  - собственные числа.

Введем обозначения:  - приближенные собственные числа, полученные Е.П.Жидковым и А.Г.Соловьевым, а  - приближенные собственные числа, полученные методом, описанным выше. Были рассчитаны собственные числа, которые представлены в таблице (см. ниже). Используя асимптотическую формулу (2.3), можно показать (достаточно грубая оценка), что

,

где  вычисляется явно. Для более точной асимптотики необходимо точно решить уравнение

.