Вычисление собственных чисел и собственных функций опрератора Штурма-Лиувилля на полуоси

Абзалимов Р.Р.

В настоящей работе предлагается метод расчета приближенных собственных чисел и собственных функций краевой задачи на полуоси для дифференциального уравнения второго порядка. Для численного расчета собственных чисел интервал заменяется на , после чего задача решается на конечном отрезке. Точность приближенных собственных чисел будет зависеть от выбора граничного условия в точке R.

I. Регулярная задача

Рассмотрим следующую краевую задачу:

,                                   (1.1)

,                                    (1.2)

.                                    (1.3)

Здесь предполагается, что q(x) кусочно-непрерывна на [a, b]. Наряду с данной задачей рассмотрим дифференциальные операторы вида:

,                                        (1.4)

с граничными условиями

,                                        (1.5)

,                                        (1.6)

где

.                                              (1.7)

Под собственными функциями краевой задачи (1.4)-(1.6) будем понимать функцию y(x), удовлетворяющую следующим условиям (см. [1]):

;

;

 удовлетворяет граничным условиям (1.5) и (1.6);

 удовлетворяет так называемым условиям сопряжения

                                              (1.8)

В каждом интервале  решения уравнения (1.4) имеют вид:

.                            (1.9)

Из условий сопряжения (1.8) и (1.9) имеем:

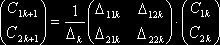,                                  (1.10)

Рекомендуем скачать другие рефераты по теме: конспект урока в школе, дипломы рефераты.





1  2  3  4  5  6  7 | Следующая страница реферата