Высшая математика

| Категория реферата: Рефераты по математике
| Теги реферата: шпоры по уголовному, оформление реферата
| Добавил(а) на сайт: Богдана.

Предыдущая страница реферата | 1 2 3 4 5 6 7 8 9 10 11 | Следующая страница реферата

Пример. Определить сходимость ряда

Вывод: ряд сходится.

Нормальные системы обыкновенных дифференциальных уравнений.

Определение. Совокупность соотношений вида:

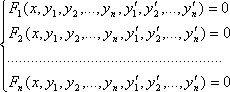
где х- независимая переменная, у1, у2,…,уn – искомые функции, называется системой дифференциальных уравнений первого порядка.

Определение. Система дифференциальных уравнений первого порядка, разрешенных относительно производных от неизвестных функций называется нормальной системой дифференциальных уравнений.

Такая система имеет вид:

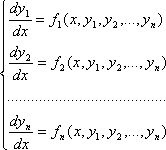(1)

Для примера можно сказать, что график решения системы двух дифференциальных уравнений представляет собой интегральную кривую в трехмерном пространстве.

Теорема. (Теорема Коши). Если в некоторой области (n-1) –мерного пространства функции … непрерывны и имеют непрерывные частные производные по , то для любой точки этой области существует единственное решение

системы дифференциальных уравнений вида (1), определенное в некоторой окрестности точки х0 и удовлетворяющее начальным условиям

Определение. Общим решением системы дифференциальных уравнений вида (1) будет совокупность функций , , … , которые при подстановке в систему (1) обращают ее в тождество

Ряды с неотрицательными членами.

При изучении знакопостоянных рядов ограничимся рассмотрением рядов с неотрицательными членами, т.к. при простом умножении на –1 из этих рядов можно получить ряды с отрицательными членами.

Теорема. Для сходимости ряда с неотрицательными членами необходимо и достаточно, чтобы частные суммы ряда были ограничены.

Признак сравнения рядов с неотрицательными членами.

Пусть даны два ряда и при un, vn ³ 0.

Теорема. Если un £ vn при любом n, то из сходимости ряда следует сходимость ряда , а из расходимости ряда следует расходимость ряда .

Доказательство. Обозначим через Sn и sn частные суммы рядов и . Т.к. по условию теоремы ряд сходится, то его частные суммы ограничены, т.е. при всех n sn < M, где М – некоторое число. Но т.к. un £ vn, то Sn £ sn то частные суммы ряда тоже ограничены, а этого достаточно для сходимости.