Предыдущая страница реферата | 2  3  4  5  6  7  8  9  10  11  12 | Следующая страница реферата

,

то ряд сходится, если же для всех достаточно больших n выполняется неравенство

то ряд расходится.

Следствие. Если существует предел , то при r<1 ряд сходится, а при r>1 ряд расходится.

Интегральный признак Коши.

Если j(х) – непрерывная положительная функция, убывающая на промежутке [1;¥), то ряд j(1) + j(2) + …+ j(n) + … =  и несобственный интеграл  одинаковы в смысле сходимости.

Пример. Ряд 1 и расходится a£1 т.к. соответствующий несобственный интеграл 1 и расходится a£1. Ряд  называется общегармоническим рядом.

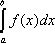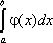Следствие. Если f(x) и j(х) – непрерывные функции на интервале (a, b] и  то интегралы  и  ведут себя одинаково в смысле сходимости.

Знакочередующиеся ряды.

Знакочередующийся ряд можно записать в виде:

где

Признак Лейбница.

Если у знакочередующегося ряда  абсолютные величины ui убывают  и общий член стремится к нулю , то ряд сходится.

Признаки Даламбера и Коши для знакопеременных рядов.

Пусть - знакопеременный ряд.

Признак Даламбера. Если существует предел 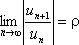, то при r<1 ряд  будет абсолютно сходящимся, а при r>1 ряд будет расходящимся. При r=1 признак не дает ответа о сходимости ряда.

Признак Коши. Если существует предел , то при r<1 ряд  будет абсолютно сходящимся, а при r>1 ряд будет расходящимся. При r=1 признак не дает ответа о сходимости ряда.

Пример. Разложить в ряд функцию

при помощи интегрирования.

При  получаем по приведенной выше формуле:

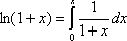
Разложение в ряд функции  может быть легко найдено способом алгебраического деления аналогично рассмотренному выше примеру.

Тогда получаем: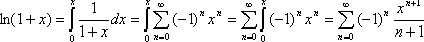

Рекомендуем скачать другие рефераты по теме: шпаргалки по уголовному, контрольные работы по математике.





Предыдущая страница реферата | 2  3  4  5  6  7  8  9  10  11  12 | Следующая страница реферата