Предыдущая страница реферата | 1  2  3  4  5  6 | Следующая страница реферата



Подставляя (3) в (2) и учитывая третье условие существования функции Лапласа имеем :

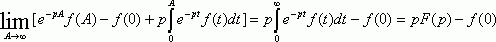
Что и требовалось доказать.

Пример: Решить дифференциальное уравнение :

  Если x(0)=0   и x’(0)=0

Предположим, что x(t) – решение в области оригиналов и , где - решение в области изображений.

       

Изображающее уравнение :

Теорема о интегрировании оригинала. Пусть  находится в области оригиналов, , тогда 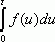также оригинал, а его изображение .

Таким образом операции интегрирования в области оригиналов соответствует операция деления в области изображений.

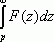Теорема о интегрировании изображений : Пусть  – функция оригинал, которая имеет изображение и  также оригинал, а - является сходящимся интегралом, тогда .

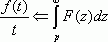Толкование теоремы : операция деления на аргумент в области оригиналов соответствует операции интегрирования в пределах от р до ¥ в области изображений.

Понятие о свертке функций. Теорема о свертке.

Пусть заданы две функции a(t) и b(t), удовлетворяющие условиям существования изображения по Лапласу, тогда сверткой таких функций называется следующая функция :

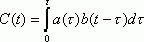            (1)

Свертка обозначается следующим образом :

                         (1’)

Равенства (1) и (1’) идентичны.

Свертка функции подчиняется переместительному закону.

Доказательство:

Рекомендуем скачать другие рефераты по теме: контрольная работа 1, доклад.

Предыдущая страница реферата | 1  2  3  4  5  6 | Следующая страница реферата