Claw.ru | Рефераты по менеджменту | Обучаемая система поддержки коллективного решения группы независимых экспертов Обучаемая система поддержки коллективного решения группы независимых экспертов | Категория реферата: Рефераты по менеджменту | Теги реферата: океан реферат, бесплатные банки рефератов | Добавил(а) на сайт: Vikul. Предыдущая страница реферата | 1  2  3  4  5  6 | Следующая страница реферата	0,05	0,01	 3 = 2
A4	0,02	0,02	0,06	 4 = 2
A5	0,01	0,05	0,04	 5 = 3

Легко видно, что в данном случае частные решения экспертов противоречивы, причем І1={1}, І2={3,4}, І3={2,5}. Для принятия коллективного решения вычислим следующие величины

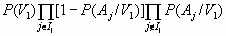= 4,03·10-8,

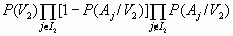= 1,12·10-6,

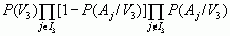= 3,73·10-6.

Поскольку третья из найденных величин максимальна, то, на основании правила (6), принимаем окончательное решение в пользу класса V3.

Частный случай коллективного решения. Рассмотрим одну из типичных задач медицинской диагностики. Требуется отнести обследуемого пациента Z к одному из двух классов: V1 – болен, V2 – здоров на основании результатов двум диагностических тестов A1, A2. При этом будем считать известными априорные вероятности P(V1), P(V2), а эффективность каждого теста, как это принято в медицинской диагностике [19], характеризовать двумя показателями: чувствительностью Qi = 1- P(Ai /V1), где вероятность P(Ai /V1) ошибочного отнесения больного пациента к здоровому и специфичностью Wi = 1- P(Ai /V2), где вероятность P(Ai /V2) ошибочного отнесения здорового пациента к больному.

Ясно, что в результате тестирования возможны четыре комбинации частных решений:

S11: δ1 = 1, δ2 = 1;

S12: δ1 = 1, δ2 = 2;

S21: δ1 = 2, δ2 = 1;

S22: δ1 = 2, δ2 = 2.

Легко видно, что в ситуациях S12 и S21 частные решения противоречивы. Для принятия коллективного решения воспользуемся правилом (6). При этом в ситуации S12, когда A1 признал Z больным, а A2 - здоровым, окончательный диагноз следует ставить согласно схеме: