Биологическое время и его моделирование в квазихимическом пространстве.

Методология построения теории времени естественных объектов, детально изложена [1, 2]. В данной работе рассмотрены компоненты этой теории на примере клеточной популяции.

1. Структура клеточной популяции. (O -компонент теории, object).

Первая проблема состоит в выборе составных частей (элементов, таксонов, униструктур) объекта и определении их пространственных границ [3, 4].

Принципиальная трудность состоит в том, что строгий критерий членения объекта на части отсутствует. Выделение объектов природы – идеализация, связанная, главным образом, с особенностями информационных взаимодействий живых организмов со средой [5].

Объективным критерием членения объекта может служить принцип энергетической дифференцировки [6], который можно записать в виде:

Еj+1j,

где Еj , Еj+1 — прочность связи между элементами уровня j и между элементами более высокого уровня j+1 (схема 1).

Для клеточной популяции порядок элементов с усложнением уровня (цифры - номера j уровней) можно представить в виде:

1 молекулы(t m)I 2 органеллы(t o) I 3 клетки (t c) I 4 популяция(t p) I 5 экосистема(t e) (1)

Каждый уровень j разбивается на подмножества элементов (схема 1).

Схема 1. Иерархия подсистем естественных объектов

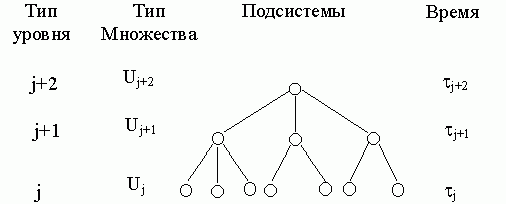
В качестве высшего уровня в данной иерархии определена экосистема. В случае клеточной монокультуры экосистема состоит из двух частей: клеточной популяции и культуральной среды. Соответственно, в описание структуры объекта необходимо вводить описание структуры среды. В частности химическая структура среды включает набор питательных веществ (субстратов) и химических агентов:

Ms = (Ms1, Ms2, ... Mse) Xs = (Xs1, X2s, ... Xse)

(2) (3)

где Ms, Xs - векторы (наборы) субстратов (Ms1, Mse) и химических агентов (Xs1,Xse) для биологического вида S.

Многомерность структуры (1-3) создает слишком большие сложности не только для количественной, но и для качественной идентификации модели. Поэтому целесообразно исследовать агрегированные модели. В случае клеточной монокультуры весьма информативной оказывается структура (1) из трех уровней:

(3) клетки I (4) популяция I (5) экосистема

(4)

Описательная модель клеточного цикла [7], начиная с митоза Cm, может быть представлена в виде разветвленной цепи:

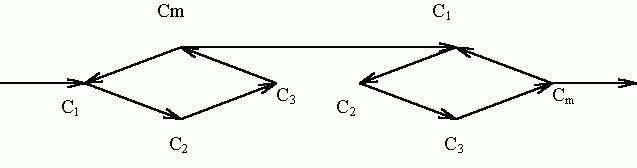
(5a)

или в более сжатом варианте:

Cm ® f C1® C2® C3® Cm

(5b)

Здесь C1 - молодая клетка непосредственно после деления, f - коэффициент размножения, который в общем случае может отличаться от 2. С2, С3, Сm - фазы развития каждой из f клеток C1.

Фазы C1, C2, C3, Cm соответствуют стадиям клеточного цикла G1, S, G2, M (клетки четырех возрастов) и являются подмножествами 4-го уровня иерархии (4) - популяции. Популяция с наборами химических агентов (2) и (3) формирует 5-й уровень модели (4).

2. Пространство допустимых состояний популяции (S-компонент теории, states).

Состояние системы отображается набором элементов (универсумов) всех типов (схема 1). В полной модели (2) состояние клеточной монокультуры задается числами всех типов мономеров, полимеров, органелл, клеток, химических и физических агентов среды. Размерность пространства состояний даже для культуры прокариотов составляет весьма большую величину.

Ограничения на достижимые состояния определяются условиями положительности числа компонентов и физической емкости среды.

В модели (4) состояние задается числами всех типов клеток, химических и физических агентов среды. Уменьшение размерности модели достигается путем аггрегирования разных элементов одного уровня по тому или иному признаку.

Например, в рассматриваемой ниже двухстадийной модели фазы C1, C2, C3 объединяются в одну по признаку их большой длительности и отсутствия деления на этих стадиях цикла. Разветвленный циклический граф, отображающий эту двухстадийную модель, имеет вид:

Рекомендуем скачать другие рефераты по теме: реферат на тему понятие, автомобили реферат доход реферат.





1  2  3  4  5  6 | Следующая страница реферата