Claw.ru | Рефераты по науке и технике | Биологическое время и его моделирование в квазихимическом пространстве Биологическое время и его моделирование в квазихимическом пространстве | Категория реферата: Рефераты по науке и технике | Теги реферата: культурология как наука, дипломная работа совершенствование | Добавил(а) на сайт: Малинов. Предыдущая страница реферата | 1  2  3  4  5  6 | Следующая страница реферата (24)

где Eb, Ep – энергии активации скоростей деления и роста, ab, ab – соответствующие предэкспоненциальные множители, T – абсолютная температура.

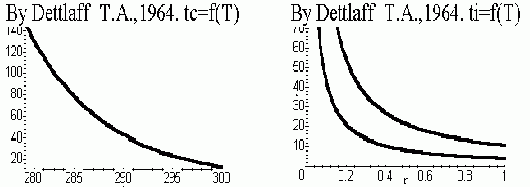
На рис. 2а приведена кривая зависимости tc , рассчитанная по уравнению (24) с помощью эмпирических параметров ab , ab и Eb, Ep. Модельная кривая качественно правильно описывает наблюдаемую закономерность [14- 16].

Подставляя аррениусовские выражения коэффициентов b и p в уравнение (20) получают формулу для расчета зависимости времени роста D t12 популяции до разных ступеней развития (разные c2/c1).

На рис. 2б приведены кривые зависимости D t12 , рассчитанные по уравнению (20) с помощью эмпирических параметров ab , ab и Eb, Ep. Модельные кривые качественно правильно описывают экспериментально наблюдаемые зависимости [14-16].

а) б)

Рис. 2. Кривые температурной зависимости длительности развития элементов разных уровней: а) длительность клеточного цикла, рассчитанная по уравнению (24); б) длительности разных стадий развития популяции, рассчитанные по уравнению (20).

Модель (12) дает возможность проверить для популяции применимость функции Бакмана [14]:

LogH = k log2T,

(25)

где H – скорость роста популяции, T – время роста, k < 0 –нормировочная постоянная.>

В аналитическом виде функцию Бакмана можно получить, подставляя в (25) выражения H и T, равные, соответственно, правым частям уравнений (14) (при w1 =0) и (16). При этом получают зависимость (25) как явную функцию роста, выражаемого переменной величиной c1 при заданном начальном значении c0. На рис. 4 приведен соответствующий график. Согласно (25), логарифм скорости роста должен быть пропорционален квадрату логарифма времени роста. Однако, как следует из рис. 4, такая зависимость для двухстадийной популяции не наблюдается.

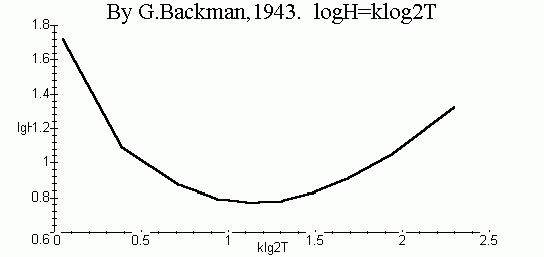
Рис. 3. Функция роста Бакмана (25), построенная на основе двухстадийной модели (16) динамики популяции.

ЛИТЕРАТУРА

1. Акчурин И.А. Единство естественнонаучного знания. М., 1974.

2. Левич А.П. // Конструкции времени в естествознании. М., 1996. С. 9-27, 235-288.

3. Шаров А.А. // Конструкции времени в естествознании. М., 1996. С. 96-111.

4. Мейен С.В. // Системность и эволюция. М., 1984. С. 7-32.

5. Ершов Ю.А.// Ж. Физ. химии. 1999. Т.73. № 10, с. 1817 – 1823.

6. Ершов Ю.А.// Ж. Физ. Химии, 2000, т. 74, № 6, с. 1087-1093.

7. Ершов Ю.А. Термодинамика квазиравновесий в биологических системах. М., ВИНИТИ, 1983. 140 с.

8. Гудвин Б. Аналитическая физиология клеток и развивающихся организмов. М.:Мир,1979,288 с.

9. Ершов Ю.А.// Докл. РАН. 1997. Т.72. № 5. с. 627-629.

10. Ершов Ю.А.// Ж. Физ. химии. 1998. Т. 352. № 3. с.553-559.

11. Ершов Ю.А. и др. Кинетика и термодинамика биохимических и физиологических процессов. М., Медицина,1990, 155с.

12. Романовский ю. м., Степанова Н.В., Чернавский Д.С. Математическая биофизика. М. Наука. 1984. - 304 с.

Рекомендуем скачать другие рефераты по теме: реферат на тему понятие, автомобили реферат доход реферат.

Предыдущая страница реферата | 1  2  3  4  5  6 | Следующая страница реферата